【頻出！公式】aPA+bPB+cPC=0(ベクトル)の点Pの位置と三角形の面積比

考え方

① 始点をそろえる

② 線分の内分・外分点の位置ベクトル

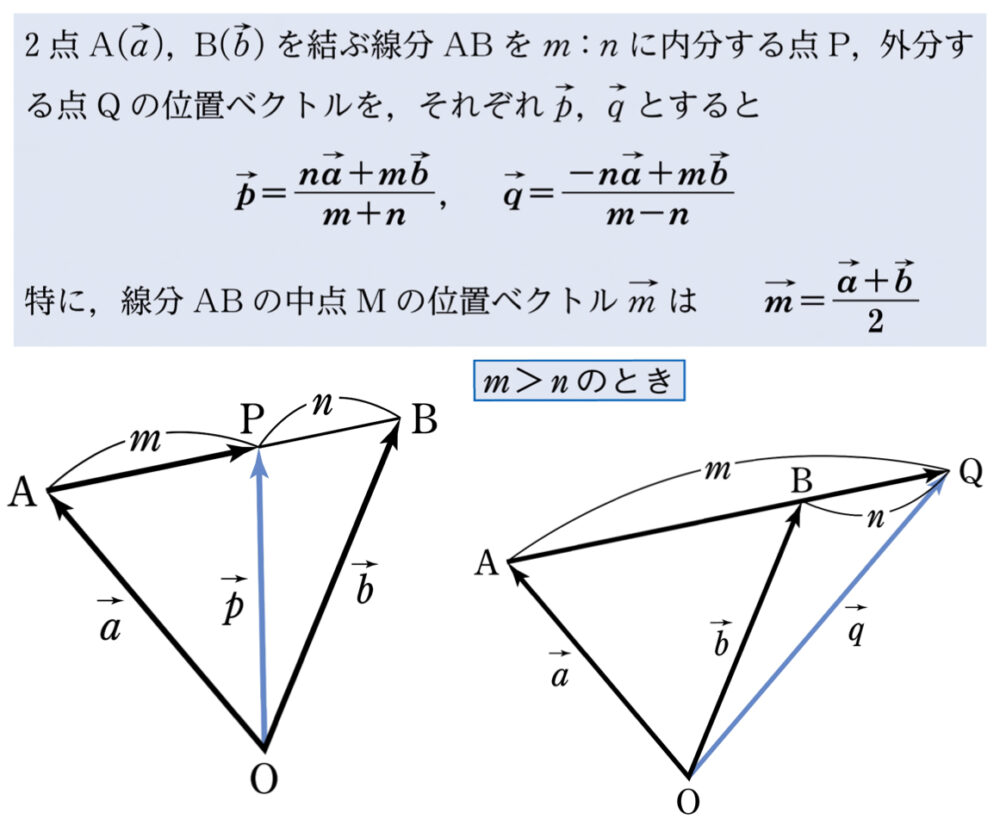
解答

(１)

$5\overrightarrow{AP}+4\overrightarrow{BP}+3\overrightarrow{CP}=\overrightarrow{0}$

始点を $A$ にそろえると

$5\overrightarrow{AP}+4(\overrightarrow{AP}-\overrightarrow{AB})+3(\overrightarrow{AP}-\overrightarrow{AC})=\overrightarrow{0}$ より

$12\overrightarrow{AP}=4\overrightarrow{AB}+3\overrightarrow{AC}$

よって $\overrightarrow{AP}=\displaystyle\frac{4\overrightarrow{AB}+3\overrightarrow{AC}}{12}$

内分点の公式が使える形に式変形をする！

Pointは，$\overrightarrow{AB}$ , $\overrightarrow{AC}$ の係数の和と，分母の値が等しくなるようにする！

$\overrightarrow{AP}=\displaystyle\frac{7}{12}\cdot\displaystyle\frac{4\overrightarrow{AB}+3\overrightarrow{AC}}{7}$ ・・・①

ここで，$\overrightarrow{AQ}=\displaystyle\frac{4\overrightarrow{AB}+3\overrightarrow{AC}}{7}$ とおく

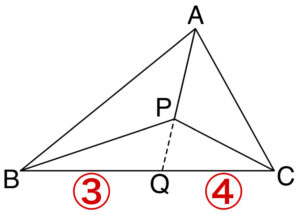
内分点の公式から点 $Q$ は $BC$ を $3 : 4$ に内分する．

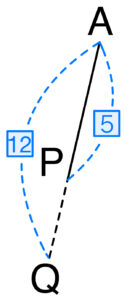
①より，$\overrightarrow{AP}=\displaystyle\frac{7}{12}\overrightarrow{AQ}$ ・・・②

②より点 $P$ は $AQ$ を $7 : 5$ に内分する点

したがって，

$BC$ を $3 : 4$ に内分する点を $Q$ とするとき，

$AQ$ を $7 : 5$ に内分する点が $P$ である．

(２)

(１) , (２)より下図のようになる．

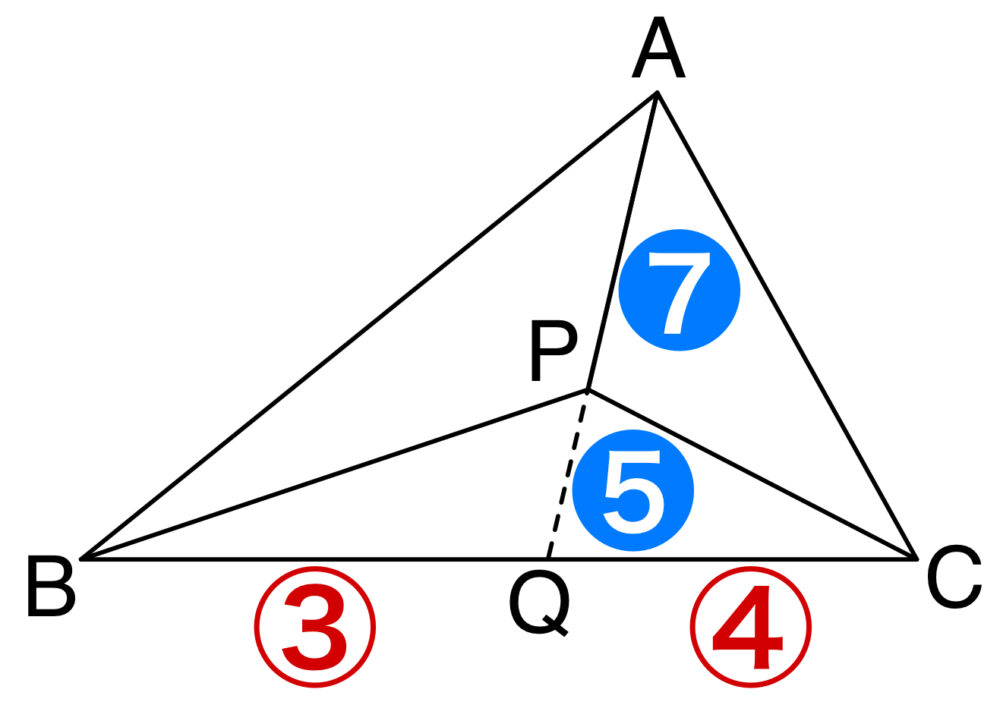
$\triangle ABC=S$ とおく．

$\triangle ABQ=\displaystyle\frac{BQ}{BC}S=\displaystyle\frac{3}{7}S$  より

$\triangle PAB=\triangle ABQ\times \displaystyle\frac{AP}{AQ}=\displaystyle\frac{3}{7}S\times \displaystyle\frac{7}{12}=\displaystyle\frac{1}{4}S$

同様に $\triangle ACQ=\displaystyle\frac{QC}{BC}S=\displaystyle\frac{4}{7}S$ より

$\triangle PCA=\displaystyle\frac{4}{7}S\times \displaystyle\frac{7}{12}=\displaystyle\frac{1}{3}S$

また，$\triangle PBC=S\times \displaystyle\frac{PQ}{AQ}=\displaystyle\frac{5}{12}S$

したがって，

$\triangle PBC : \triangle PCA : \triangle PAB=\displaystyle\frac{5}{12}S : \displaystyle\frac{1}{3}S : \displaystyle\frac{1}{4}S=5 : 4 : 3$

頻出！覚えておくべき公式！

記述の模試・テストにおいては上記のようにしっかりと途中過程が必要ですが，共通テストや私大入試のようなマーク形式(答えのみOK)であれば，次の公式は頻出ですので結果を覚えておきましょう！

$5\overrightarrow{AP}+4\overrightarrow{BP}+3\overrightarrow{CP}=\overrightarrow{0}$ より

係数に注目すると，$\triangle PBC : \triangle PCA : \triangle PAB=5 : 4 : 3$