【1993神戸大学・理(後期)】
座標空間において,\(4\) 点 \(O ( 0 , 0 , 0 )\) , \(A ( 2 , 2 , 2 )\) , \(B ( 1 , 3 , 1 )\) , \(C ( -2 , 4 , 2 )\) を考える.次の各問に答えなさい.
(1) \(3\) 点 \(A\) , \(B\) , \(C\) を通る平面の方程式を求めなさい.
(2) 点 \(( 30 , 20 , -50 )\) に光源を置く.このとき,四面体 \(OABC\) の面 \(ABC\) に光があたるかどうかを理由をつけて答えなさい.
(1)平面の方程式
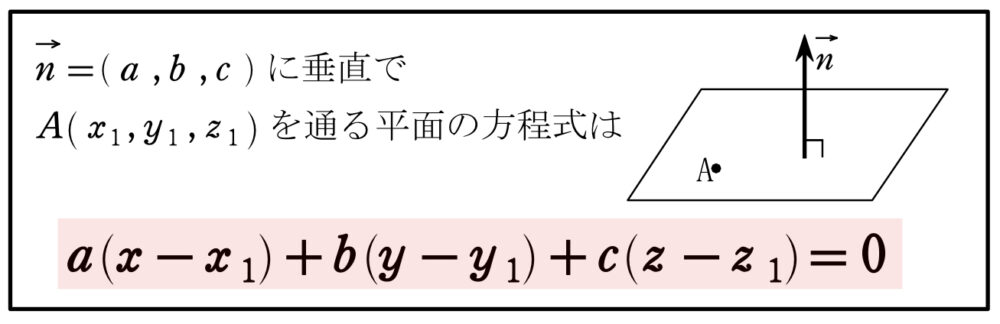
平面の方程式の証明,\(\overrightarrow{n}\) の求め方については「平面の方程式・点と平面の距離・空間上の直線の方程式・外積の公式まとめ・例題演習」を参考にしてください。外積についても紹介しています。
(1)解答
\(\overrightarrow{AB}=(-1,1,-1)\) , \(\overrightarrow{AC}=(-4,2,0)=2(-2,1,0)\) の両方に垂直なベクトルの\(1\) つを \(\overrightarrow{n}\) とおくと,\(\overrightarrow{n}=(1,2,1)\) ・・・(※)

\(\overrightarrow{AB}\) , \(\overrightarrow{AC}\) の両方に垂直なベクトルの求め方については,「平面の方程式・点と平面の距離・空間上の直線の方程式・外積の公式まとめ・例題演習」を参考に!外積についても紹介しています!
したがって求める平面の方程式は,
\((x-2)+2(y-2)+(z-2)=0\) \(\iff\) \(x+2y+z-8=0\)
(2)正領域と負領域
正領域・負領域とは?
平面上の曲線 \(f(x,y)=0\) において,平面は \(2\) つに分けられる.このとき,
\(f(x,y)>0\) となる領域を正領域,\(f(x,y)<0\) となる領域を負領域 という.
正領域・負領域について具体的な例題や考え方は「【差がつく】正領域と負領域の例題と考え方|数学Ⅱ:図形と方程式」をご参考にください。

(2)考え方
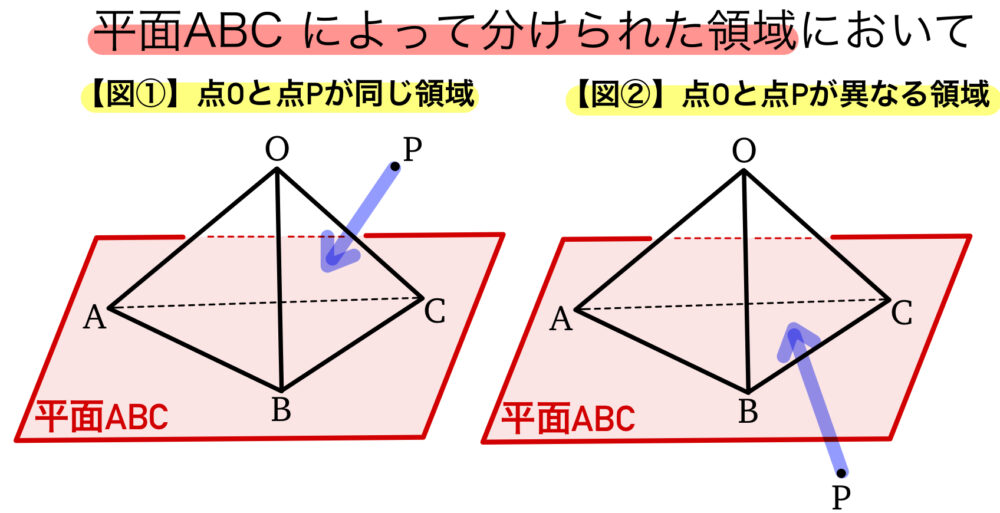
題意を満たすためには,【図②】のようになればよい.
つまり,平面 \(ABC\) によって分けられた領域の一方に点 \(O\) , もう一方に点 \(P\) がくれば良い.
⇒ 点 \(O\) , \(P\) の一方が正領域,もう一方が負領域
解答
空間は,平面 \(ABC\) : \(x+2y+z-8=0\) によって \(2\) つの領域
\(x+2y+z-8>0\) ・・・①
\(x+2y+z-8<0\) ・・・②
に分かれる.
\(O ( 0 , 0 , 0 )\) においては,\(x+2y+z-8=-8<0\)
点 \(( 30 , 20 , -50 )\) においては,\(x+2y+z-8=12>0\)
であるから,四面体 \( OABC\) の内部の点はすべて領域②に含まれ,光源は領域①に含まれるので,面 \(ABC\) に光は当たる.






コメント