【2021名古屋大学(文理共通)】
\(4\) つの実数を \(\alpha=\log_{2}{3}\) , \(\beta=\log_{3}{5}\) , \(\gamma=\log_{5}{2}\) , \(\delta=\displaystyle\frac{3}{2}\) とおく.以下の問に答えよ.
(1) \(\alpha\beta\gamma=1\) を示せ.
(2) \(\alpha\) , \(\beta\) , \(\gamma\) , \(\delta\) を小さい順に並べよ.
(3) \(p=\alpha+\beta+\gamma\) , \(q=\displaystyle\frac{1}{\alpha}+\displaystyle\frac{1}{\beta}+\displaystyle\frac{1}{\gamma}\) とし,\(f(x)=x^3+px^2+qx+1\) とする.このとき,\(f\left(-\displaystyle\frac{1}{2}\right)\) , \(f(-1)\) および \(f\left(-\displaystyle\frac{3}{2}\right)\) の正負を判定せよ.
考え方と解答・解説
(1) 底の変換公式

(1)解答
\(\beta\) , \(\gamma\) の底を \(2\) にそれぞれ変換すると
\(\beta=\displaystyle\frac{\log_{2}{5}}{\log_{2}{3}}\) , \(\gamma=\displaystyle\frac{1}{\log_{2}{5}}\) より
\(\alpha\beta\gamma=\log_{2}{3}\times \displaystyle\frac{\log_{2}{5}}{\log_{2}{3}}\times \displaystyle\frac{1}{\log_{2}{5}}=1\)
(2) 対数の大小比較

\(4\) つを同時に比較するのは難しいので,明らかに小さい(または大きい)ものを調べよう!
\(\alpha=\log_{2}{3}>\log_{2}{2}=1\) ,
\(\beta=\log_{3}{5}>\log_{3}{3}=1\) ,
\(\gamma=\log_{5}{2}<\log_{5}{5}=1\) ,
\(\delta=\displaystyle\frac{3}{2}>1\) であるから,
\(\gamma\) が一番小さいことがわかる!

残り \(\alpha\) , \(\beta\) , \(\delta\) の大小を考えれば良いが,
\(\alpha\) , \(\beta\) を直接比較するのは難しいので,
「\(\alpha\) と \(\delta\) の大小」,「\(\beta\) と \(\delta\) の大小」
をそれぞれ考えよう!
(2)解答
・\(\alpha\) と \(\delta\) の大小関係について
\(\delta=\displaystyle\frac{3}{2}=\log_{2}{2^{\frac{3}{2}}}=\log_{2}{2\sqrt{2}}\) より
\(3>2\sqrt{2}\) であるから,\(\alpha>\delta\) ・・・①
・\(\beta\) と \(\delta\) の大小関係について
\(\delta=\displaystyle\frac{3}{2}=\log_{3}{3^{\frac{3}{2}}}=\log_{3}{3\sqrt{3}}\) より
\(5<3\sqrt{3}\) であるから,\(\beta<\delta\) ・・・②
また,
\(0<\log_{5}{2}<\log_{5}{5}=1=\log_{3}{3}<\log_{3}{5}\) より
\(\gamma<\beta\) ・・・③
①,②,③より
\(\gamma<\beta<\delta<\alpha\)
(3)解答
\(q=\displaystyle\frac{1}{\alpha}+\displaystyle\frac{1}{\beta}+\displaystyle\frac{1}{\gamma}=\displaystyle\frac{\alpha\beta+\beta\gamma+\gamma\alpha}{\alpha\beta\gamma}\)
(1)から \(\alpha\beta\gamma=1\) より
\(q=\alpha\beta+\beta\gamma+\gamma\alpha\)
よって,
\(f(x)=x^3+(\alpha+\beta+\gamma)x^2+(\alpha\beta+\beta\gamma+\gamma\alpha)x+\alpha\beta\gamma\)
\(=(x+\alpha)(x+\beta)(x+\gamma)\)
したがって,\(y=f(x)\) と \(x\) 軸との共有点の \(x\) 座標は
\(x=-\alpha , -\beta , -\gamma\)
(2)より
\(0<\gamma<1<\beta<\delta=\displaystyle\frac{3}{2}<\alpha\) であるから
\(-\alpha<-\displaystyle\frac{3}{2}<-\beta<-1<-\gamma<0\)
よって \(y=f(x)\) のグラフの概形は下図のようになる
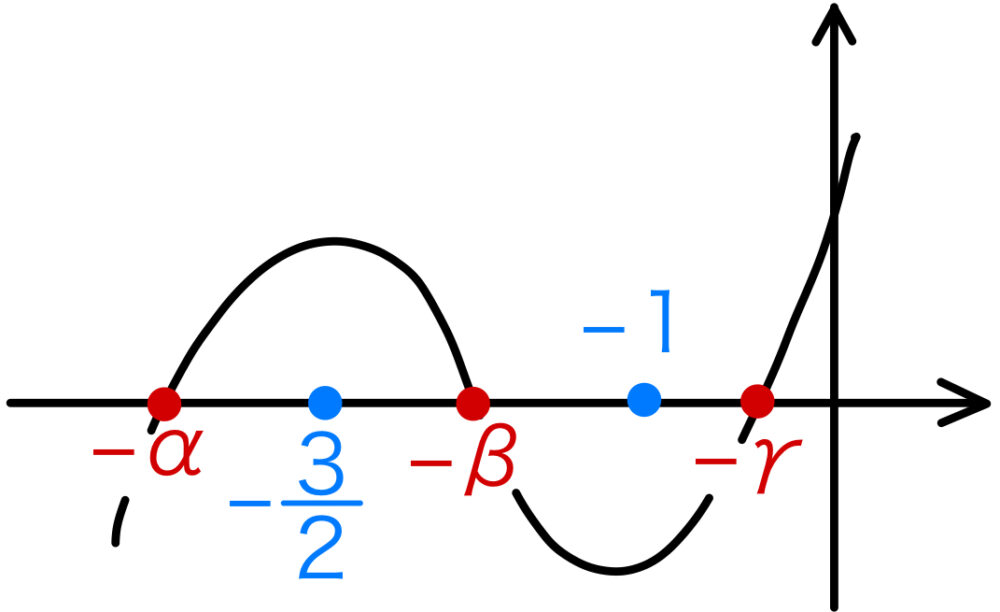
グラフより,\(f\left(-\displaystyle\frac{3}{2}\right)>0\) , \(f(-1)<0\)

\(f\left(-\displaystyle\frac{1}{2}\right)\) の正負を調べるためには,
\(\displaystyle\frac{1}{2}\) と \(\gamma\) の大小関係
つまり,\(-\displaystyle\frac{1}{2}\) と \(-\gamma\) の大小関係を調べればよい!
ここで,\(\displaystyle\frac{1}{2}=\log_{5}{5^{\frac{1}{2}}}=\log_{5}{\sqrt{5}}\) で
\(2<\sqrt{5}\) より,\(\gamma<\displaystyle\frac{1}{2}\)
よって,\(-\displaystyle\frac{1}{2}<-\gamma\) であるから
上のグラフより,\(f\left(-\displaystyle\frac{1}{2}\right)<0\)







コメント