【2022数学ⅡB第５問平面ベクトル】

(１)問題と解答・解説

(１)解答・解説

$\overrightarrow{OA}\cdot\overrightarrow{OB}=\left|\overrightarrow{OA}\right|\left|\overrightarrow{OB}\right|\cos\angle AOB$ であり，

$\left|\overrightarrow{OA}\right|=\left|\overrightarrow{OB}\right|=1$ ， $\overrightarrow{OA}\cdot\overrightarrow{OB}=-\displaystyle\frac{2}{3}$ より

$\cos\angle AOB=-\displaystyle\frac{2}{3}$ ・・・《アイウ》

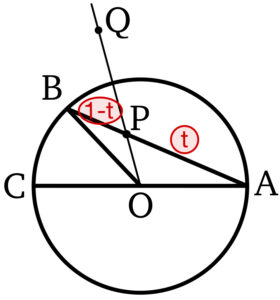
次に，点 $P$ は線分 $AB$ を $t : 1-t$ に内分するので，

$\overrightarrow{OP}=(1-t)\overrightarrow{OA}+t\overrightarrow{OB}$

となる．よって実数 $k$ を用いて， $\overrightarrow{OQ}=k\overrightarrow{OP}$ と表せるので，

$\overrightarrow{OQ}=(k-kt)\overrightarrow{OA}+kt\overrightarrow{OB}$ ・・・《エ：① , オ：⓪》

$\overrightarrow{CQ}=\overrightarrow{OQ}-\overrightarrow{OC}=\overrightarrow{OQ}+\overrightarrow{OA}$ より

$\overrightarrow{CQ}=(k-kt+1)\overrightarrow{OA}+kt\overrightarrow{OB}$ ・・・《カ：④ , キ：⓪》

$\overrightarrow{OA}\perp\overrightarrow{OP}$ $\iff$ $\overrightarrow{OA}\cdot\overrightarrow{OP}=0$ より

$\overrightarrow{OA}\cdot\left\{(1-t)\overrightarrow{OA}+t\overrightarrow{OB}\right\}=0$

$(1-t)\left|\overrightarrow{}\right|^2+t\overrightarrow{OA}\cdot\overrightarrow{OB}=0$

$1-t-\displaystyle\frac{2}{3}t=0$

よって， $t=\displaystyle\frac{3}{5}$ ・・・《クケ》

(２)問題と解答・解説

(２)解答・解説

$\angle OCQ$ が直角のとき

$\overrightarrow{OC}\cdot\overrightarrow{CQ}=0$

$-\overrightarrow{OA}\cdot\left\{(k-kt+1)\overrightarrow{OA}+kt\overrightarrow{OB}\right\}=0$

$-(k-kt+1)\left|\overrightarrow{OA}\right|^2-kt\overrightarrow{OA}\cdot\overrightarrow{OB}=0$

$-k+kt-1+\displaystyle\frac{2}{3}kt=0$

$(5t-3)k=3$

$t\not=\displaystyle\frac{3}{5}$ より， $k=\displaystyle\frac{3}{5t-3}$ ・・・《コサシ》

$\angle OCQ$ が直角であるから，

点 $Q$ は点 $O$ を中心とした半径 $1$ の円における

点 $C$ での接線上にある

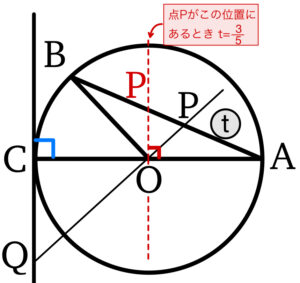
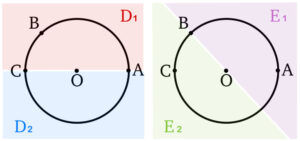
( ⅰ )　 $0<t<\displaystyle\frac{3}{5}$ のとき

$0°<\angle AOP<90°$ より

点 $Q$ は ③ $D_{2}$ に含まれ，かつ $E_{2}$ に含まれる・・・《ス》

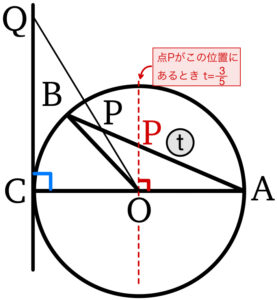
( ⅱ )　 $\displaystyle\frac{3}{5}<t<1$ のとき

$90°<\angle AOP<\angle AOB$ より

点 $Q$ は ⓪ $D_{1}$ に含まれ，かつ $E_{1}$ に含まれる・・・《セ》

(３)問題と解答・解説

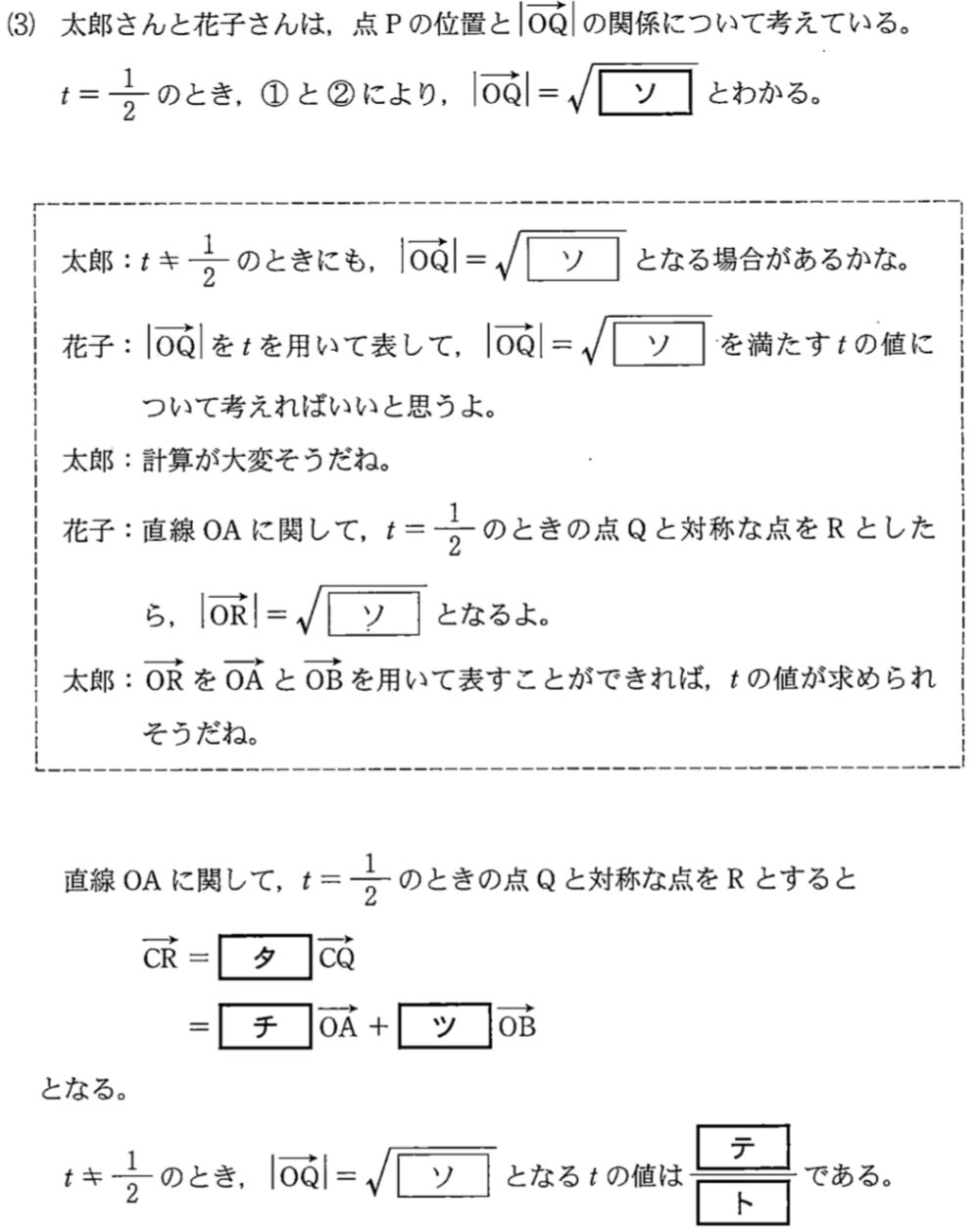
(３)解答・解説

$t=\displaystyle\frac{1}{2}$ のとき $k=\displaystyle\frac{3}{5k-3}$ より

$k=-6$ である．

よって， $\overrightarrow{OQ}=-6\overrightarrow{OP}$ より

$\overrightarrow{OQ}=-6\left(\displaystyle\frac{1}{2}\overrightarrow{OA}+\displaystyle\frac{1}{2}\overrightarrow{OB}\right)$

$=-3\overrightarrow{OA}-3\overrightarrow{OB}$

$\left|\overrightarrow{OQ}\right|^2=9\left(\left|\overrightarrow{OA}\right|^2+2\overrightarrow{OA}\cdot\overrightarrow{OB}+\left|\overrightarrow{OB}\right|^2\right)=6$

したがって， $\left|\overrightarrow{OQ}\right|=\sqrt{6}$ ・・・《ソ》

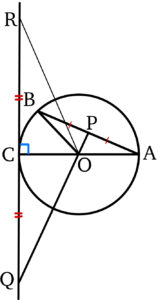
直線 $OA$ に関して， $t=\displaystyle\frac{1}{2}$ のとき点 $Q$ と対称な点を $R$ とすると，

$\overrightarrow{CR}=-\overrightarrow{CQ}$ ・・・《タ》

$=-\left(\overrightarrow{OQ}-\overrightarrow{OC}\right)$

$=-\overrightarrow{OQ}+\overrightarrow{OC}$

$=2\overrightarrow{OA}+3\overrightarrow{OB}$ ・・・《チツ》

これが (１) で求めた $\overrightarrow{CQ}=(k-kt+1)\overrightarrow{OA}+kt\overrightarrow{OB}$ と一致するとき， $\overrightarrow{OA}$ と $\overrightarrow{OB}$ は一次独立なベクトルであるから，

$\begin{cases}k-kt+1=2\\kt=3\end{cases}$

よって， $k=4$ , $t=\displaystyle\frac{3}{4}$ ・・・《テト》