【2022大阪医科薬科大学・看護・[4]】

解答・解説
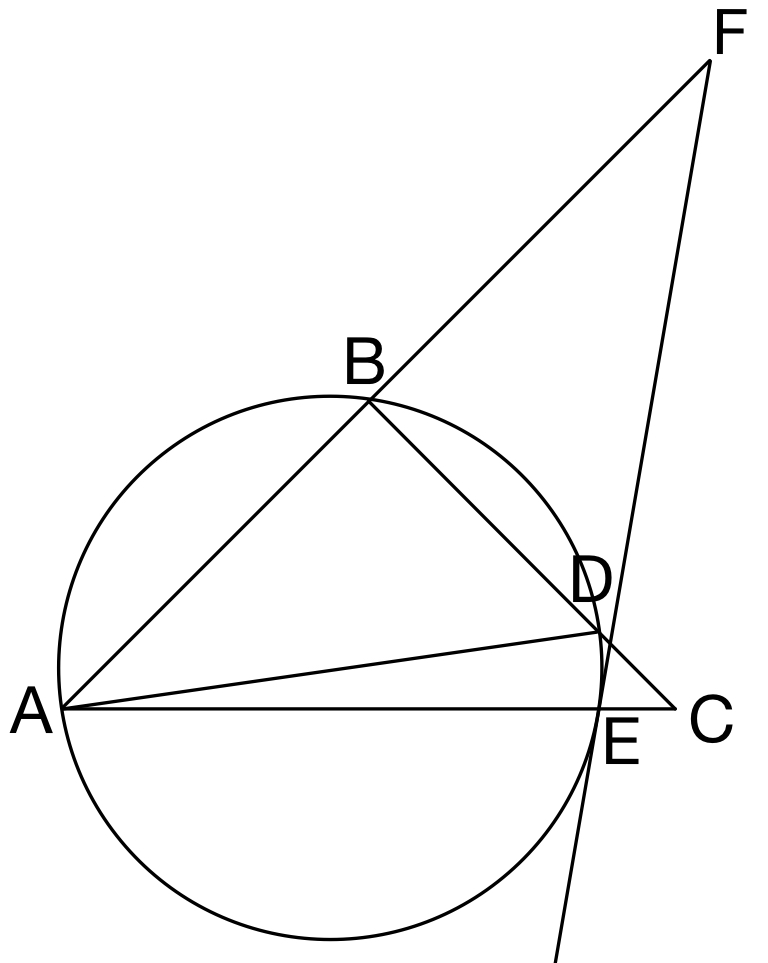
(1) 方べきの定理
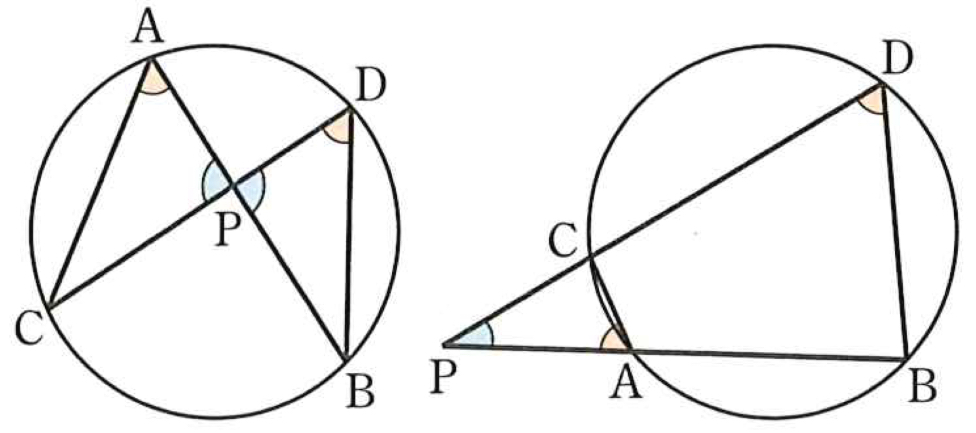 方べきの定理
方べきの定理
円の \(2\) つの弦 \(AB\) , \(CD\) の交点,またはそれらの延長上の交点を \(P\) とすると,
\(PA\cdot PB=PC\cdot PD\)
方べきの定理より
\(CD\times CB=CE\times CA\)
\(2\times 8=CE\times 8\sqrt{2}\)
よって,\(CE=\sqrt{2}\) ・・・( c )
(2) 接弦定理
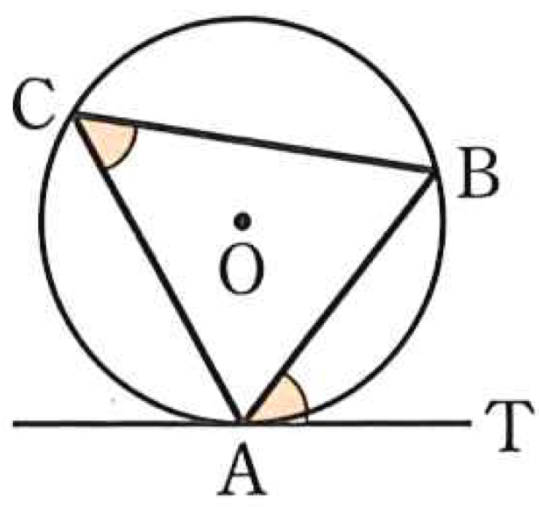 接線と弦の作る角(接弦定理)
接線と弦の作る角(接弦定理)
円 \(O\) の弦 \(AB\) と,その端点 \(A\) における
接線 \(AT\) が作る角 \(\angle BAT\) は,
その角の内部に含まれる孤 \(AB\) に対する円周角 \(\angle ACB\) に等しい.
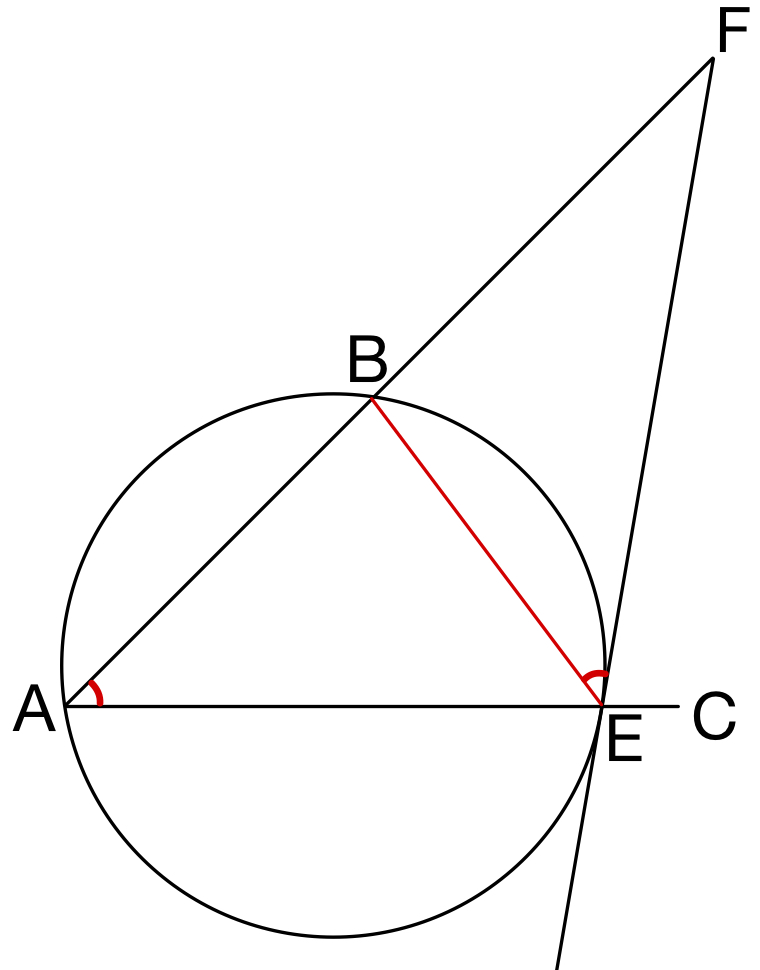 (※右図は分かりやすいように不要な点や線分を削除した図)
(※右図は分かりやすいように不要な点や線分を削除した図)
接弦定理より
\(\angle EAB=\angle BEF\) ・・・( d )
(3) 余弦定理
 余弦定理
余弦定理
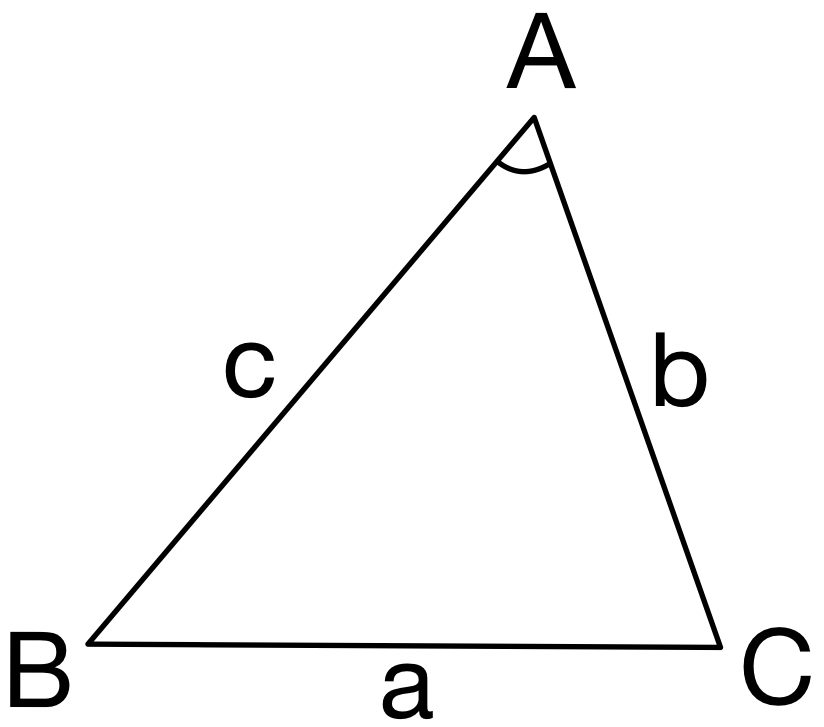
\(\triangle ABC\) において
・\(a^2=b^2+c^2-2bc\cos A\)
・\(\cos A=\displaystyle\frac{b^2+c^2-a^2}{2bc}\)
\(AB=BC\) であり,
\(AB:BC:AC=1:1:\sqrt{2}\) より
\(\triangle ABC\) は \(\angle B=90°\) の直角二等辺三角形となる.
よって,\(\angle EAB=45°\)
また,\(AE=AC-CE=7\sqrt{2}\)
\(\triangle ABE\) で余弦定理から
\(BE^2=8^2+(7\sqrt{2})^2-2\times 8\times 7\sqrt{2}\cos 45°=50\)
\(BE>0\) より,\(BE=5\sqrt{2}\) ・・・( c )
(4) 相似な三角形
 \(\angle F\) は共通で,(2) より \(\angle EAB=\angle BEF\) であるから,
\(\angle F\) は共通で,(2) より \(\angle EAB=\angle BEF\) であるから,
\(\triangle FBE\) と \(\triangle FEA\) は相似な三角形となる.
ここで \(FB=x\) ,\(FE=y\) とおく.
\(FB:BE=FE:EA\) かつ \(FE:BE=FA:EA\)
\(\iff\) \(x:5\sqrt{2}=y:7\sqrt{2}\) かつ \(y:5\sqrt{2}=(x+8):7\sqrt{2}\)
\(\iff\) \(5y=7x\) かつ \(5x+40=7y\)
これを解くと,\(y=\)\(EF=\displaystyle\frac{35}{3}\) ・・・( e )








コメント