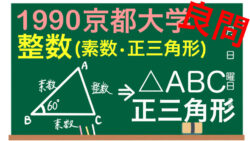
 整数問題
整数問題 1990京都大学【整数問題・素数】B=60、bは整数、a、cは素数のとき、△ABCは正三角形
素数は積の形に弱い。余弦定理から積の形に変形。数学A整数問題。2次試験対策。良問。過去問題演習。
 整数問題
整数問題  集合と命題
集合と命題  集合と命題
集合と命題  図形と方程式
図形と方程式  ベクトル
ベクトル  集合と命題
集合と命題  2次関数
2次関数  ベクトル
ベクトル  2次関数
2次関数  数と式
数と式  集合と命題
集合と命題  数と式
数と式  数と式
数と式  共通テスト(センター試験)
共通テスト(センター試験)  三角関数
三角関数  数と式
数と式  数と式
数と式  東京大学
東京大学  式と証明
式と証明  2次関数
2次関数  集合と命題
集合と命題  分野まとめ
分野まとめ 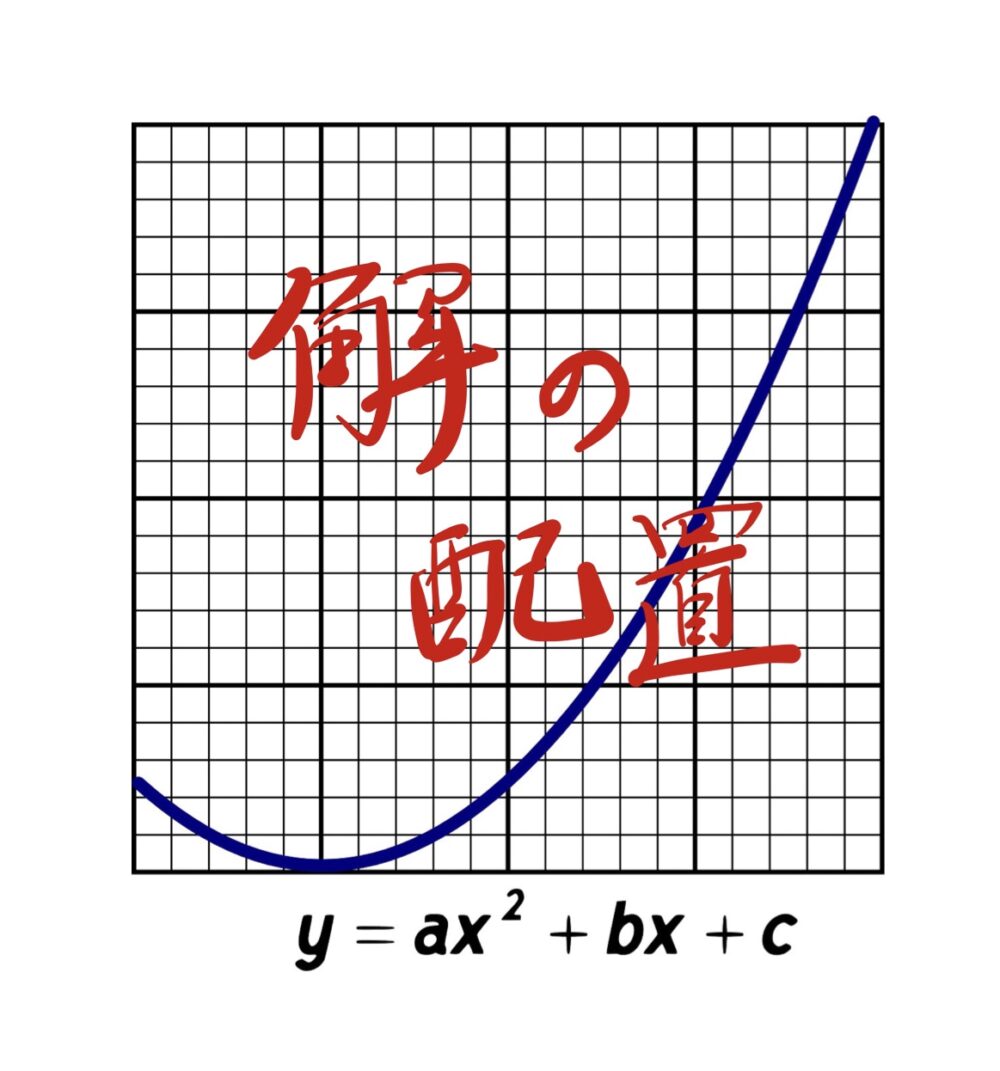 2次関数
2次関数 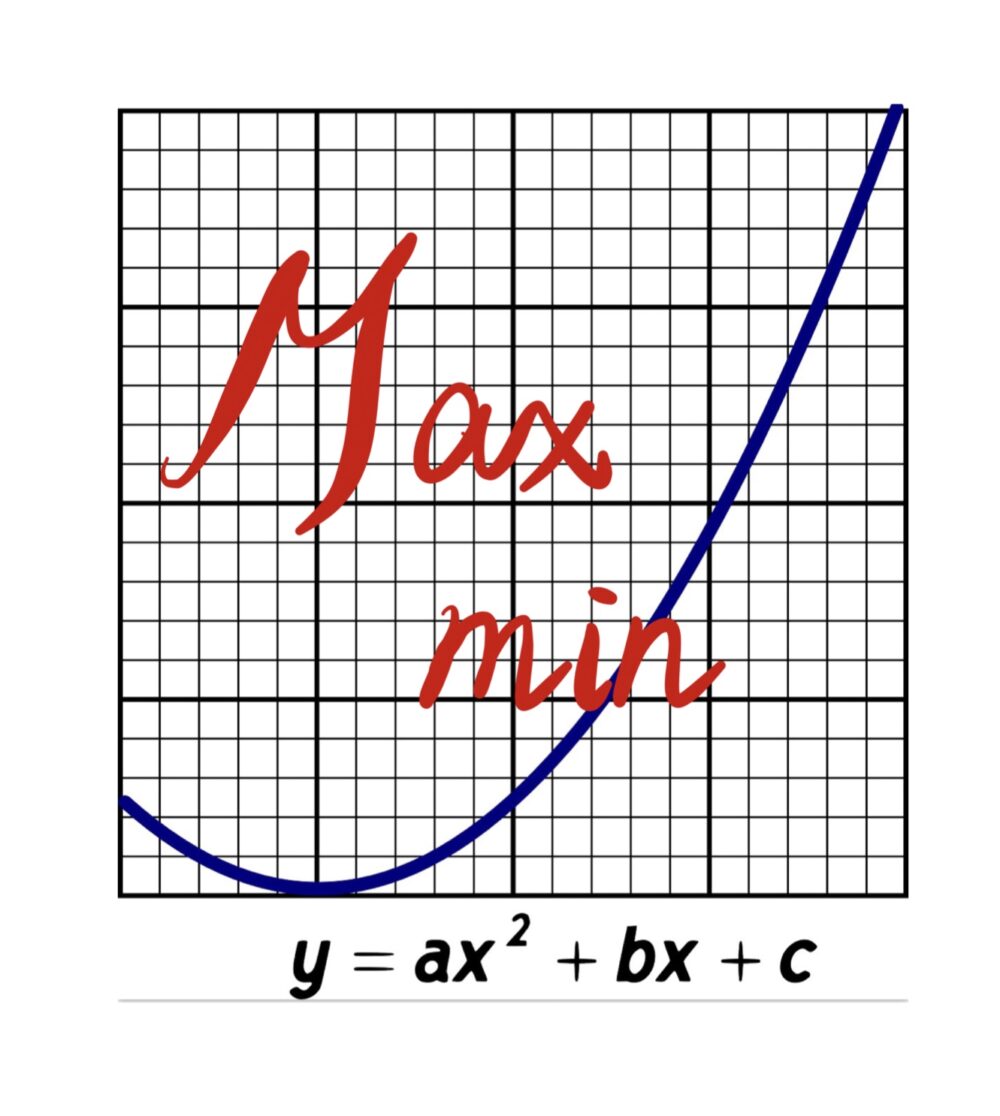 2次関数
2次関数