 2024年入試問題
2024年入試問題 【2024神戸大学・文系・第1問】3次関数の最小値、対数型の漸化式
3次関数の最小値。分数型の漸化式、隣接二項間特性方程式型など、典型タイプの漸化式。誘導あり。2024神戸大学・文科・第1問(数学Ⅱ微分、数学B数列)。問題・解答・解説速報。神大過去問演習。
 2024年入試問題
2024年入試問題 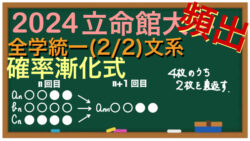 2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  漸化式
漸化式  漸化式
漸化式  数列
数列  数列
数列  漸化式
漸化式  共通テスト(センター試験)
共通テスト(センター試験)  数列
数列  数列
数列  数列
数列  数列
数列  漸化式
漸化式  漸化式
漸化式  式と証明
式と証明  数列
数列  漸化式
漸化式  数列
数列  数列
数列  数列
数列  数列
数列  数列
数列