\(0\text{°}≦\theta≦90\text{°}\) のとき
\(\displaystyle\frac{\sin\theta+1}{\cos\theta+1}\)
のとり得る値の範囲を求めよ.
![]()
考え方(解答にたどり着くために)
1.媒介変数の利用
媒介変数って何??しっかりと理解できていない人は、
を参考にしてください.
2.\(k\) についての恒等式
【例題】\(k\) を定数とする.
直線 \((k+1)x-(2k+3)y-3k-5=0\) は、\(k\) の値に関わらず定点を通る.
その定点の座標を求めよ.
\(( A )+( B )k=0\) の形に変形
➡ \(A = 0\) かつ \(B = 0\)
直線 \((k+1)x-(2k+3)y-3k-5=0\) を \(k\) についてまとめると、
\((x-3y-5)+(x-2y-3)k=0\)
これが \(k\) の値に関わらず成立するとき、
\(x-3y-5=0\) かつ \(x-2y-3=0\)
これを解くと、\(( x , y )=( -1 , -2 )\)
3.線形計画法
【例題】
\(x^2+y^2=1\) のとき、\(y-x\) のとり得る値の範囲を求めよ.
\(y-x=k\) とおく.
\(y=x+k\) ・・・① より
傾きが \(1\)、\(y\) 切片が \(k\) の直線を表す.
\(x^2+y^2=1\) (中心原点、半径 \(1\) の円) と、①が交点を持つ範囲を考えると下図のようになり、
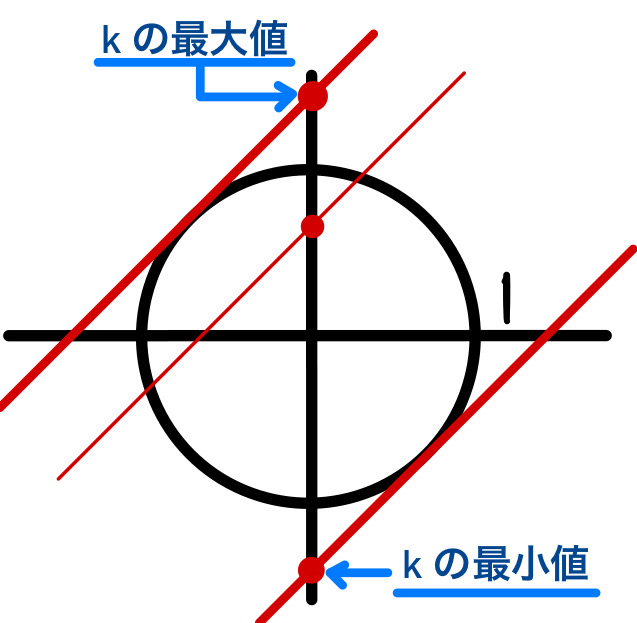
\(k\) (\(y\) 切片) が最大、最小となるのは、それぞれ①が円と接するときである.
(計算は省略)
したがって、\(-\sqrt{2}≦k≦\sqrt{2}\)
つまり、\(-\sqrt{2}≦y-x≦\sqrt{2}\)
![]()
解答
\(0\text{°}≦\theta≦90\text{°}\) のとき
\(\displaystyle\frac{\sin\theta+1}{\cos\theta+1}\)
のとり得る値の範囲を求めよ.
\(x=\cos\theta\) 、\(y=\sin\theta\) \((0\text{°}≦\theta≦90\text{°})\) とおく.
このとき \(( x , y )\) は、
\(x^2+y^2=1\)、\(x≧0\)、\(y≧0\) ・・・ ① を表す.
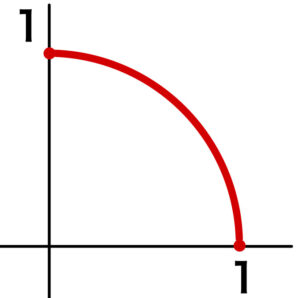
このとき、
\(\displaystyle\frac{\sin\theta+1}{\cos\theta+1}=k\) とおくと、
\(k=\displaystyle\frac{y+1}{x+1}\)
\(y+1=k(x+1)\) ・・・ ②
②は \(k\) の値に関わらず、\(( x , y )=( -1 , -1 )\) を通り、傾き \(k\) の直線を表す.
つまり本問は、①と②が共有点をもつときの \(k\) (傾き) の範囲を考えればよい.
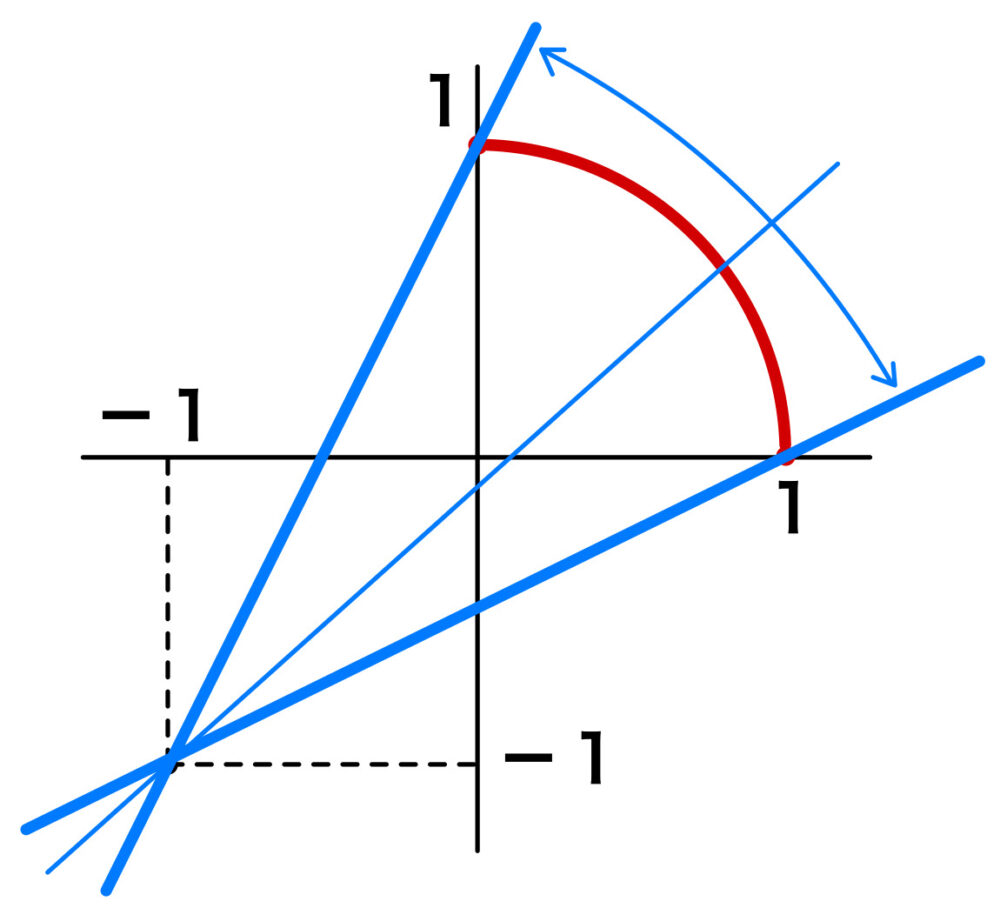
図より、
②が \(( 1 , 0 )\) を通るとき、\(k=\displaystyle\frac{1}{2}\)
\(( 0 , 1 )\) を通るとき、\(k=2\)
したがって、\(\displaystyle\frac{1}{2}≦k≦2\)
つまり、\(\displaystyle\frac{1}{2}≦\displaystyle\frac{\sin\theta+1}{\cos\theta+1}≦2\)








コメント