【2021数学ⅠA】第1問[2](図形と計量)
(1)問題と解答・解説《セ〜テ》
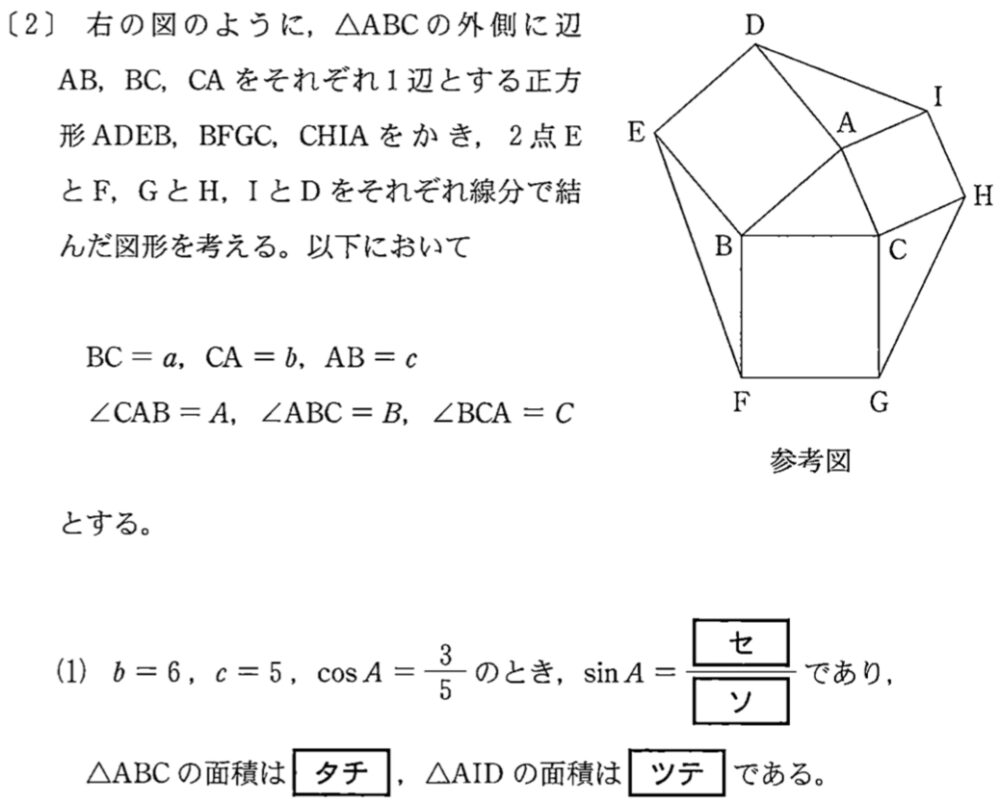
(1)解答・解説《セ〜テ》
\(\sin A=\sqrt{1-\cos^2A}=\sqrt{1-\left(\displaystyle\frac{3}{5}\right)}^2=\)\(\displaystyle\frac{4}{5}\) ・・・《セソ》
よって,\(\triangle ABC=\displaystyle\frac{1}{2}bc\sin A=\displaystyle\frac{1}{2}\times 6\times 5\times \displaystyle\frac{4}{5}=\)\(12\) ・・・《タチ》
また,\(\angle DAI=180°-A\) より,\(\sin \angle DAI=\sin A\)
したがって,\(\triangle AID=\displaystyle\frac{1}{2}bc\sin A=\triangle ABC=\) \(12\) ・・・《ツテ》
(2)問題と解答・解説《ト〜ニ》
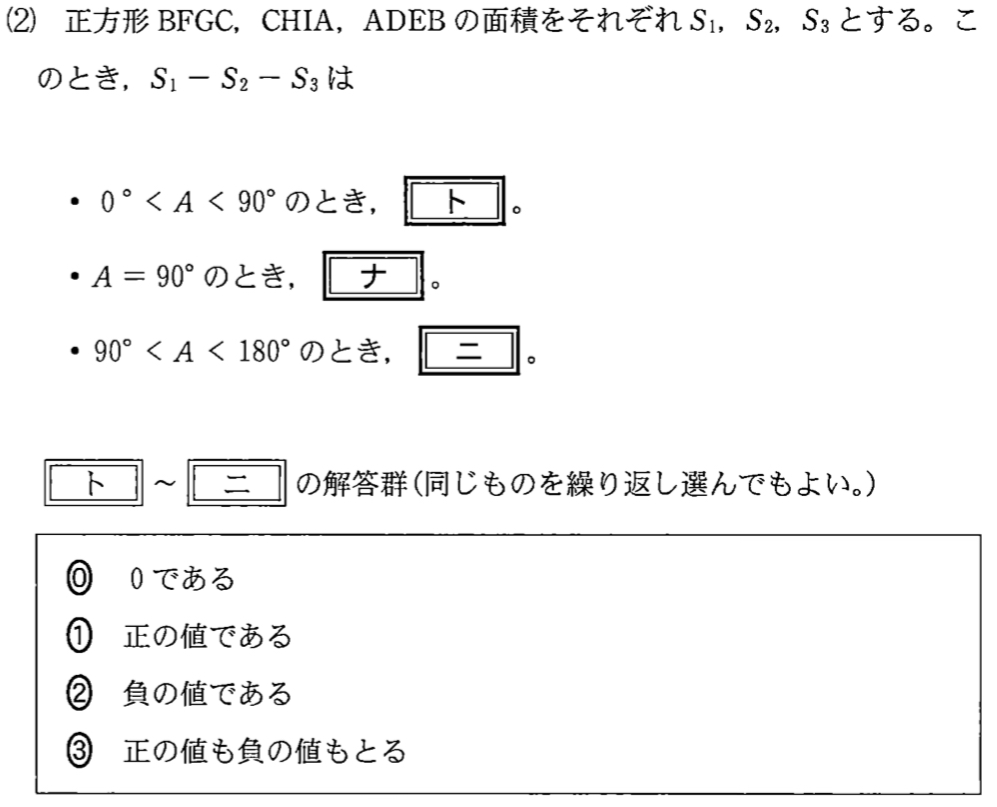
(2)解答・解説《ト〜ニ》
\(S_{1}=a^2\) , \(S_{2}=b^2\) , \(S_{3}=c^2\) となる.
・\(0°<A<90°\) のとき
\(a^2<b^2+c^2\) より \(a^2-b^2-c^2<0\)
よって,\(S_{1}-S_{2}-S_{3}<0\) ・・・《ト:②》
・\(A=90°\) のとき
\(a^2=b^2+c^2\) より \(a^2-b^2-c^2=0\)
よって,\(S_{1}-S_{2}-S_{3}=0\) ・・・《ナ:⓪》
・\(90°<A<180°\) のとき
\(a^2>b^2+c^2\) より \(a^2-b^2-c^2>0\)
よって,\(S_{1}-S_{2}-S_{3}>0\) ・・・《ニ:①》
(3)問題と解答・解説《ヌ》

(3)解答・解説《ヌ》
(1)と同様に考えると,
\(\triangle BEF=\triangle ABC\) , \(\triangle CGH=\triangle ABC\) であるから,
\(a\) , \(b\) , \(c\) の値に関係なく,\(T_{1}=T_{2}=T_{3}\) ・・・《ヌ:③》
(4)問題と解答・解説《ネ〜ヒ》
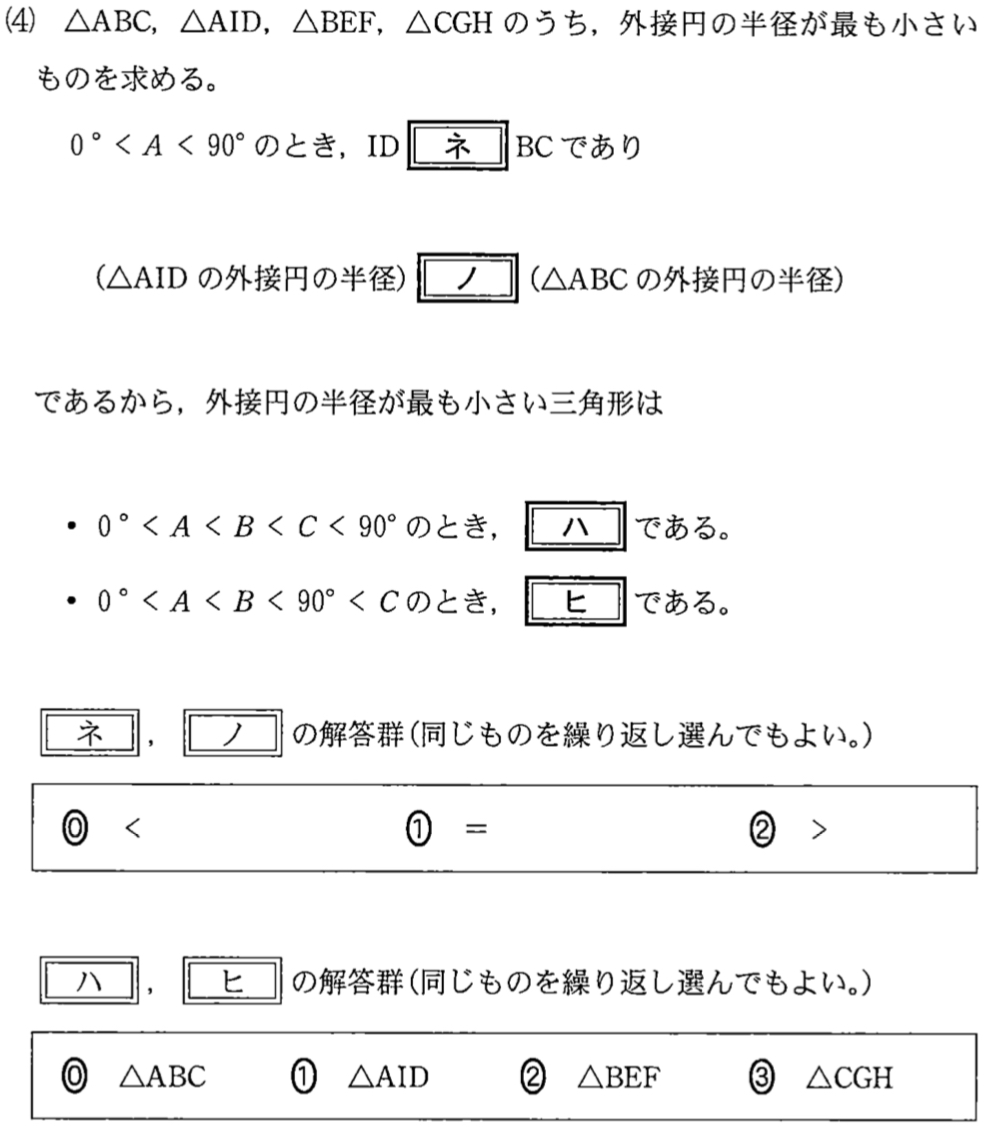
(4)解答・解説《ネ〜ヒ》
\(0°<A<90°\) のとき
\(\angle IAD=180°-A\) より,\(90°<\angle IAD<180°\)
\(\triangle ABC\) において(2)より,\(a^2<b^2+c^2\)
\(\triangle AID\) において(2)より,\(ID^2>b^2+c^2\)
よって \(ID^2>a^2=BC^2\) であるから \(ID>BC\) ・・・《ネ:②》
ここで,\(\triangle ABC\) , \(\triangle AID\) の外接円の半径をそれぞれ \(R\) , \(R_{1}\) とすると正弦定理から,
\(2R_{1}=\displaystyle\frac{ID}{\sin IAD}=\displaystyle\frac{ID}{\sin (180°-A)}=\displaystyle\frac{ID}{\sin A}\)
\(2R=\displaystyle\frac{BC}{\sin A}\) であるから,\(ID>BC\) より \(R_{1}>R\) ・・・《ノ:②》
次に,\(\triangle BEF\) , \(\triangle CGH\) の外接円の半径をそれぞれ \(R_{2}\) , \(R_{3}\) とすると,
・\(0°<A<B<C<90°\) のとき
上と同様に考え,\(R_{2}>R\) , \(R_{3}>R\) となる.
よって,\(R\) が最も小さい ・・・《ハ:⓪》
・\(0°<A<B<90°<C\) のとき
\(0°<A<B<90°\) より,\(R_{1}>R\) , \(R_{2}>R\)
また,\(90°<C\) より \(R>R_{3}\) となるので,
\(R_{3}\) が最も小さい ・・・《ヒ:③》








コメント