【2021数学ⅡB(第1日程)】第4問(数列)

(1)問題と解答・解説《ア〜ク》
解答・解説《ア〜ク》
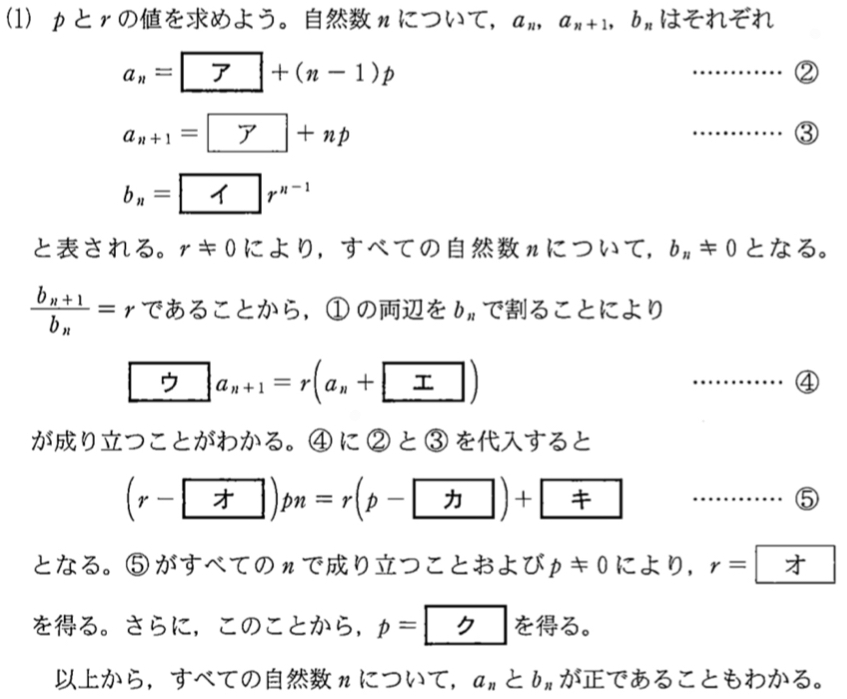
数列 \(\left\{a_{n}\right\}\) は初項が \(3\) , 公差が \(p\) の等差数列より
\(a_{n}=3+(n-1)p\) ・・・《ア》
これより,\(a_{n+1}=3+np\)
また,数列 \(\left\{b_{n}\right\}\) は初項が \(3\) , 公比が \(r\) の等比数列より
\(b_{n}=3r^{n-1}\) ・・・《イ》
\(r\not=0\) により,すべての自然数 \(n\) について \(b_{n}\not=0\) となるので
\(r=\displaystyle\frac{b_{n+1}}{b_{n}}\) であることから,
\(a_{n}b_{n+1}-2a_{n+1}b_{n}+3b_{n+1}=0\) の両辺を \(b_{n}\) で割ると
\(\displaystyle\frac{a_{n}b_{n+1}}{b_{n}}-2a_{n+1}+3\displaystyle\frac{b_{n+1}}{b_{n}}=0\)
よって,\(ra_{n}-2a_{n+1}+3r=0\)
\(2a_{n+1}=r(a_{n}+3)\) ・・・《ウエ》
\(2(3+np)=r\left\{3+(n-1)p+3\right\}\)
\((r-2)pn=r(p-6)+6\) ・・・《オ〜キ》
これがすべての自然数 \(n\) で成り立つこと,および \(p\not=0\) より
\(r-2=0\) かつ \(r(p-6)+6=0\)
\(\iff\) \(r=2\) , \(p=3\) ・・・《ク》
(2)問題と解答・解説《ケ〜ス》
解答・解説《ケ〜ス》
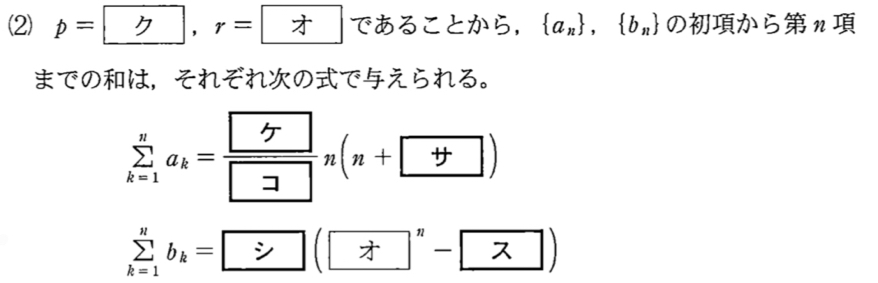
\(p=3\) のとき \(a_{n}=3+3(n-1)=3n\) より
\(\displaystyle\sum_{k=1}^{n}{a_{k}}=\displaystyle\sum_{k=1}^{n}{3k}=\)\(\displaystyle\frac{3}{2}n(n+1)\) ・・・《ケ〜サ》
\(r=2\) のとき \(b_{n}=3\cdot2^{n-1}\) より
\(\displaystyle\sum_{k=1}^{n}{b_{k}}=\displaystyle\sum_{k=1}^{n}{3\cdot2^{n-1}}=\displaystyle\frac{3(2^n-1)}{2-1}=\)\(3(2^n-1)\) ・・・《シス》
(3)問題と解答・解説《セ〜タ》

解答・解説《セ〜タ》
\(a_{n}c_{n+1}-4a_{n+1}c_{n}+3c_{n+1}=0\) より
\((a_{n}+3)c_{n+1}=4a_{n}c_{n}\)
\(a_{n}>0\) より \(a_{n}+3>0\) であるから,
\(c_{n+1}=\displaystyle\frac{4a_{n}}{a_{n}+3}c_{n}\) ・・・《セソ》
\(p=3\) のとき,\(a_{n}=3n\) , \(a_{n+1}=3(n+1)\) なので
\(c_{n+1}=\displaystyle\frac{4\times 3(n+1)}{3n+3}c_{n}=4c_{n}\)
よって,数列 \(\left\{c_{n}\right\}\) は ② 公比が \(1\) より大きい等比数列・・・《タ》
(4)問題と解答・解説《チ〜テ》

解答・解説《チ〜テ》
\(d_{n}b_{n+1}-qd_{n+1}b_{n}+ub_{n+1}=0\)
\(b_{n}\not=0\) なので両辺を \(b_{n}\) で割ると
\(\displaystyle\frac{d_{n}b_{n+1}}{b_{n}}-qd_{n+1}+\displaystyle\frac{ub_{n+1}}{b_{n}}=0\)
\(\displaystyle\frac{b_{n+1}}{b_{n}}=r=2\) より
\(2d_{n}-qd_{n+1}+2u=0\)
よって,\(d_{n+1}=\displaystyle\frac{2}{q}(d_{n}+u)\) ・・・《チ》
したがって,数列 \(\left\{d_{n}\right\}\) が公比が \(0\) より大きく \(1\) より小さい等比数列となるための必要十分条件は,
\(0<\displaystyle\frac{2}{q}<1\) かつ \(u=0\)
\(\iff\) \(q>2\) かつ \(u=0\) ・・・《ツテ》









コメント