【2022数学ⅠA】第5問(図形の性質)
(1)問題と解答・解説《ア〜ケ》
解答・解説《ア〜ケ》
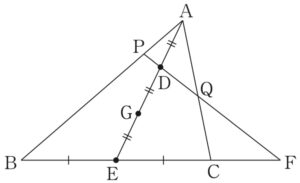
点 \(G\) は \(\triangle ABC\) の重心より,
\(AG:GE=2:1\) であり,
点 \(D\) が \(AG\) の中点のとき
\(AD=DG=GE\) となる.
よって,\(\displaystyle\frac{AD}{DE}=\displaystyle\frac{1}{2}\) ・・・《アイ》
\(\triangle ABE\) と直線 \(PD\) に関してメネラウスの定理より
\(\displaystyle\frac{BP}{PA}\cdot\displaystyle\frac{AD}{DE}\cdot\displaystyle\frac{EF}{FB}=1\)
\(\displaystyle\frac{BP}{PA}\cdot\displaystyle\frac{1}{2}\cdot\displaystyle\frac{EF}{FB}=1\)
よって,\(\displaystyle\frac{BP}{AP}=2\times \displaystyle\frac{BF}{EF}\) ・・・《ウ〜オ》
\(\triangle AEC\) と直線 \(DQ\) に関してメネラウスの定理より
\(\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AD}{DE}\cdot\displaystyle\frac{EF}{FC}=1\)
\(\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{1}{2}\cdot\displaystyle\frac{EF}{FC}=1\)
よって,\(\displaystyle\frac{CQ}{AQ}=2\times \displaystyle\frac{CF}{EF}\) ・・・《カ〜ク》
\(\displaystyle\frac{BP}{AP}+\displaystyle\frac{CQ}{AQ}=2\times \displaystyle\frac{BF}{EF}+2\times \displaystyle\frac{CF}{EF}=2\times \displaystyle\frac{BF+CF}{EF}\)
点 \(E\) は辺 \(BC\) の中点なので,\(BF+CF=2EF\) であるから
\(\displaystyle\frac{BP}{AP}+\displaystyle\frac{CQ}{AQ}=\)\(4\) ・・・《ケ》
(2)問題と解答・解説《コ〜ナ》
解答・解説《コ〜ナ》
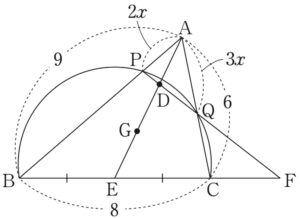
方べきの定理より
\(AP\cdot AB=AQ\cdot AC\) であるから
\(9AP=6AQ\)
よって,\(AQ=\displaystyle\frac{3}{2}AP\) ・・・《コサ》
\(AP=2x\) とおくと,\(AQ=3x\) であり,(1)の結果から
\(\displaystyle\frac{BP}{AP}+\displaystyle\frac{CQ}{AQ}=4\) なので
\(\displaystyle\frac{9-2x}{2x}+\displaystyle\frac{6-3x}{3x}=4\)
これを解くと,\(x=\displaystyle\frac{13}{12}\)
よって,\(AP=2x=\)\(\displaystyle\frac{13}{6}\) ・・・《シ〜セ》
\(AQ=3x=\)\(\displaystyle\frac{13}{4}\) ・・・《ソ〜チ》
(1)の \(\displaystyle\frac{BP}{AP}=2\times \displaystyle\frac{BF}{EF}\) より
\(\displaystyle\frac{9-\frac{13}{6}}{\frac{13}{6}}=2\times \displaystyle\frac{8+CF}{4+CF}\)
これを解くと,\(CF=\displaystyle\frac{44}{15}\) ・・・《ツ〜ナ》
(3)問題と解答・解説《二〜ヌ》

解答・解説《二〜ヌ》
\(\displaystyle\frac{AD}{DE}=k\) とおく.
(1)と同様に考え
\(\displaystyle\frac{BP}{AP}=\displaystyle\frac{1}{k}\times \displaystyle\frac{BF}{EF}\) ,
\(\displaystyle\frac{CQ}{AQ}=\displaystyle\frac{1}{k}\times \displaystyle\frac{CF}{EF}\)
であり,
\(\displaystyle\frac{BP}{AP}+\displaystyle\frac{CQ}{AQ}=\displaystyle\frac{1}{k}\displaystyle\frac{BF+CF}{EF}=\displaystyle\frac{2}{k}\)
よって,\(\displaystyle\frac{2}{k}=10\) \(\iff\) \(k=\displaystyle\frac{1}{5}\)
したがって,\(AD:DG:GE=1:3:2\) であるから,
\(\displaystyle\frac{AD}{DG}=\displaystyle\frac{1}{3}\) ・・・《二ヌ》








コメント