【2021数学ⅠA(第２日程)】第１問[２](図形と計量)

(１)問題と解答・解説《キ〜コ》

(１)解答・解説《キ〜コ》

正弦定理より

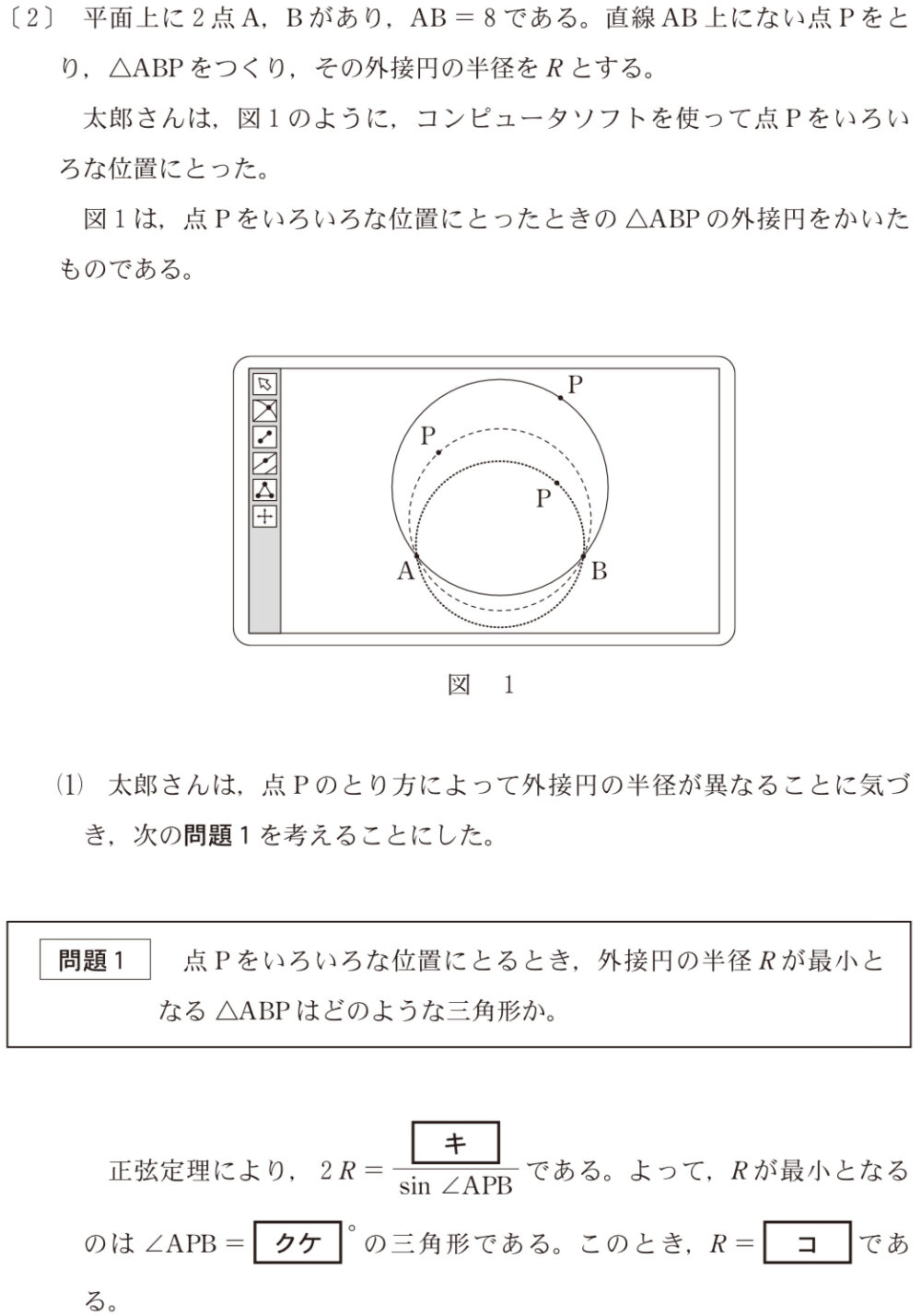
\(2R=\displaystyle\frac{AB}{\sin\angle APB}=\)\(\displaystyle\frac{8}{\sin\angle APB}\) ・・・《キ》

であるから，\(R=\displaystyle\frac{4}{\sin\angle APB}\)

これが最小となるのは，\(\sin\angle APB\) が最大となるときである．

よって，\(\sin\angle APB=1\) のとき

つまり，\(\angle APB=90°\) ・・・《クケ》

このとき，\(R=4\) ・・・《コ》

(２)問題と解答・解説《サ》

(２)解答・解説《サ》

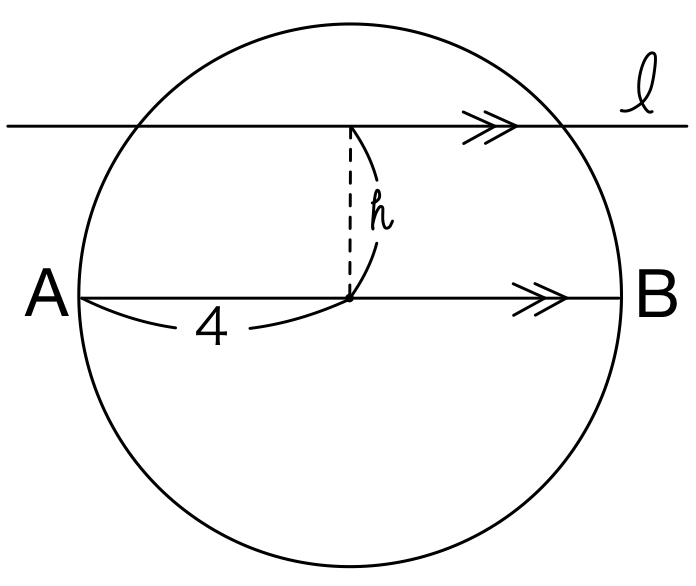
円 \(C\) は線分 \(AB=8\) を直径とする円なので，半径は \(4\) である．

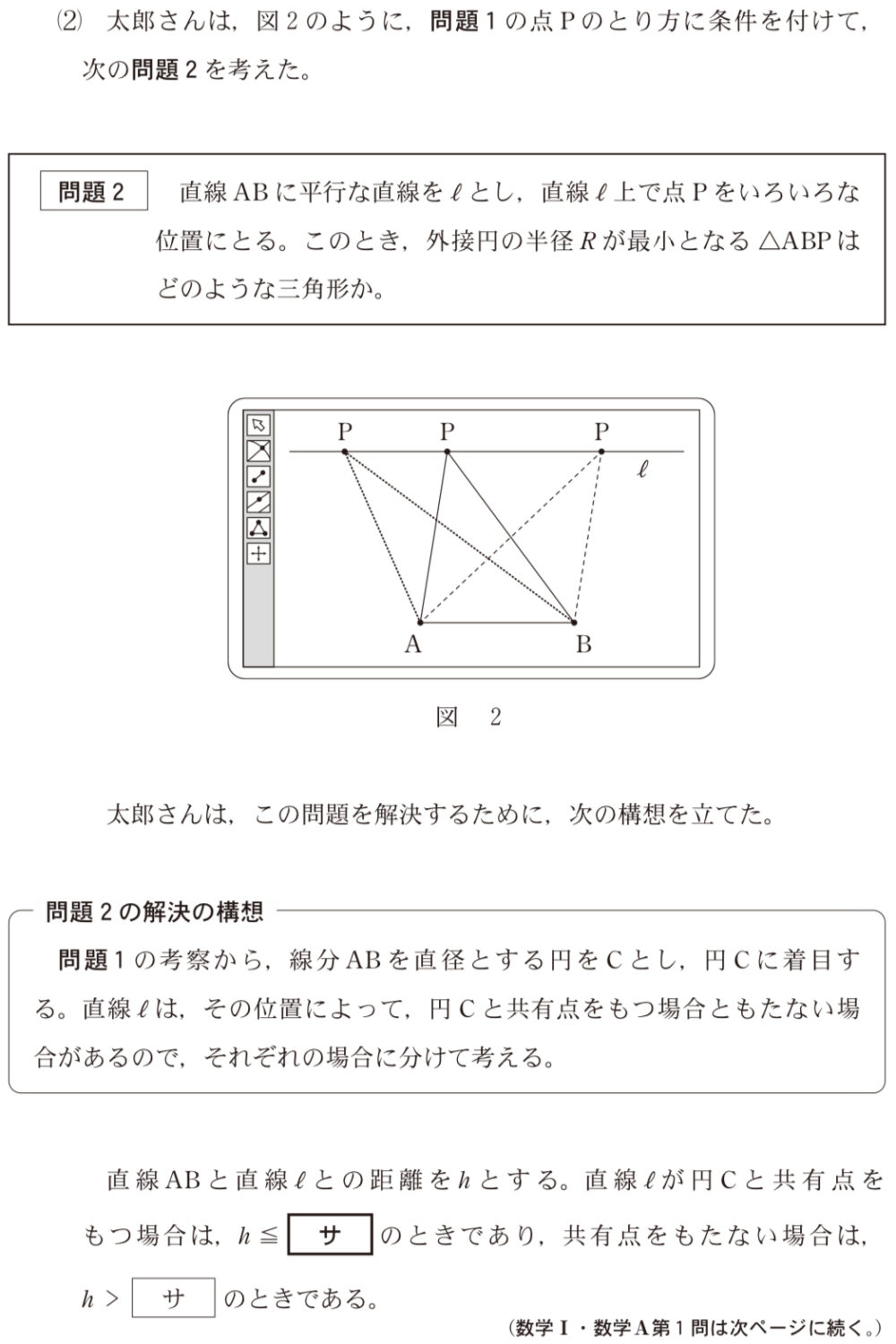
直線 \(l\) が円 \(C\) と共有点をもつのは，円 \(C\) の半径と，円 \(C\) の中心から直線 \(l\) までの距離 ( \(h\) ) に注目すると

\(h≦4\) ・・・《サ》のとき．

また共有点を持たない場合は，\(h>4\) のときである．

(２)問題と解答・解説《シ〜タ》

(２)解答・解説《シ〜タ》

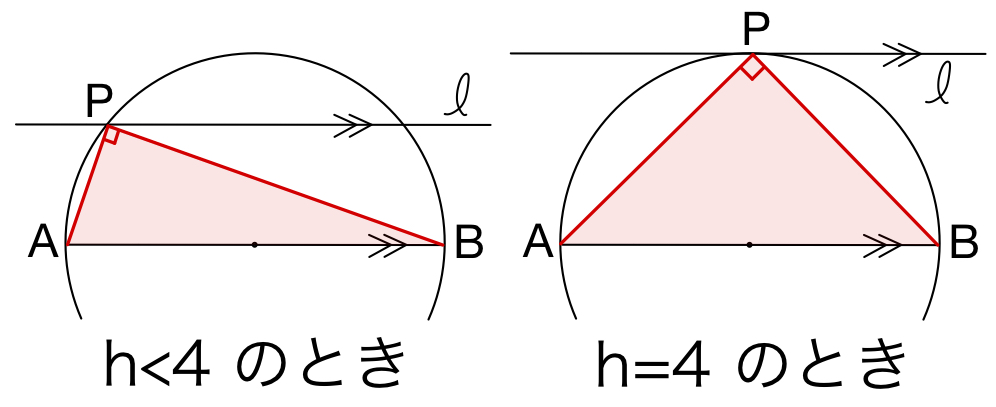
( ⅰ )　\(h≦4\) のとき

直線 \(l\) が円 \(C\) と共有点をもつので，

\(R\) が最小となるのは， \(\triangle ABP\) は

上図より

・\(h<4\) のとき，①直角三角形 ・・・《シ》

・\(h=4\) のとき，直角二等辺三角形　である．

( ⅱ )　\(h>4\) のとき

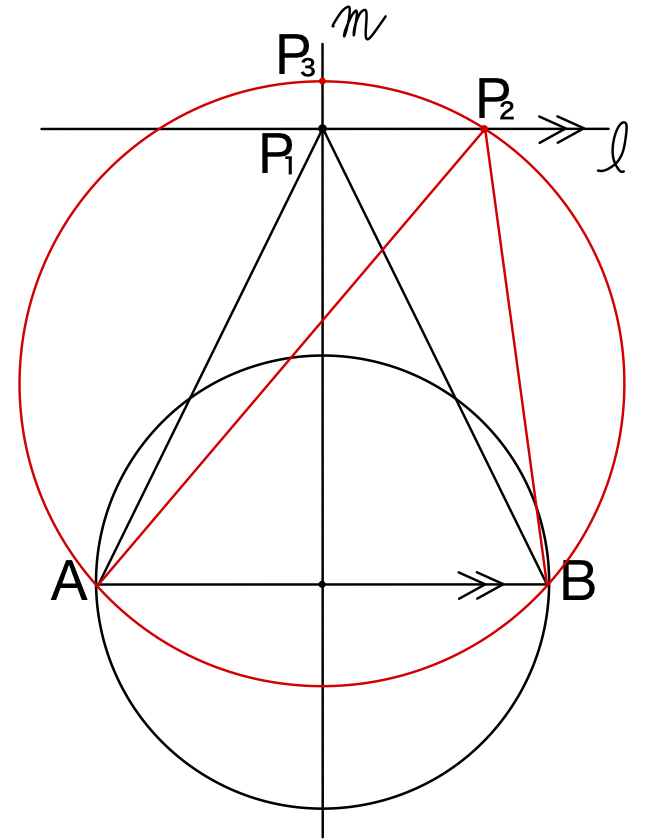
円周角の定理から，\(\angle AP_{3}B=\angle AP_{2}B\) ・・・《ス：①》

また，\(\angle AP_{3}B<\angle AP_{1}B<90°\) より

\(\sin \angle AP_{3}B<\sin\angle AP_{1}B\) ・・・《セ：⓪》

このとき，\(\triangle ABP_{1}\) と \(\triangle ABP_{2}\) の外接円の半径をそれぞれ \(R_{1}\) ，\(R_{2}\) とおくと，正弦定理より

\(2R_{1}=\displaystyle\frac{AB}{\sin\angle AP_{1}B}=\displaystyle\frac{8}{\sin\angle AP_{1}B}\)

\(2R_{2}=\displaystyle\frac{AB}{\sin\angle AP_{2}B}=\displaystyle\frac{8}{\sin\angle AP_{2}B}=\displaystyle\frac{8}{\sin\angle AP_{3}B}\)

\(\sin \angle AP_{3}B<\sin\angle AP_{1}B\) より

\(\displaystyle\frac{8}{\sin\angle AP_{3}B}>\displaystyle\frac{8}{\sin\angle AP_{1}B}\)

つまり \(2R_{2}>2R_{1}\)

よって，\(R_{1}<R_{2}\) ・・・《ソ：⓪》

さらに，\(R\) が最小となるのは \(\triangle ABP\) は \(AP_{1}=BP_{1}\) の \(\triangle ABP_{1}\) である．

したがって，\(R\) が最小となるのは ③二等辺三角形 ・・・《タ》である．

(３)問題と解答・解説《チ〜テ》

(３)解答・解説《チ〜テ》

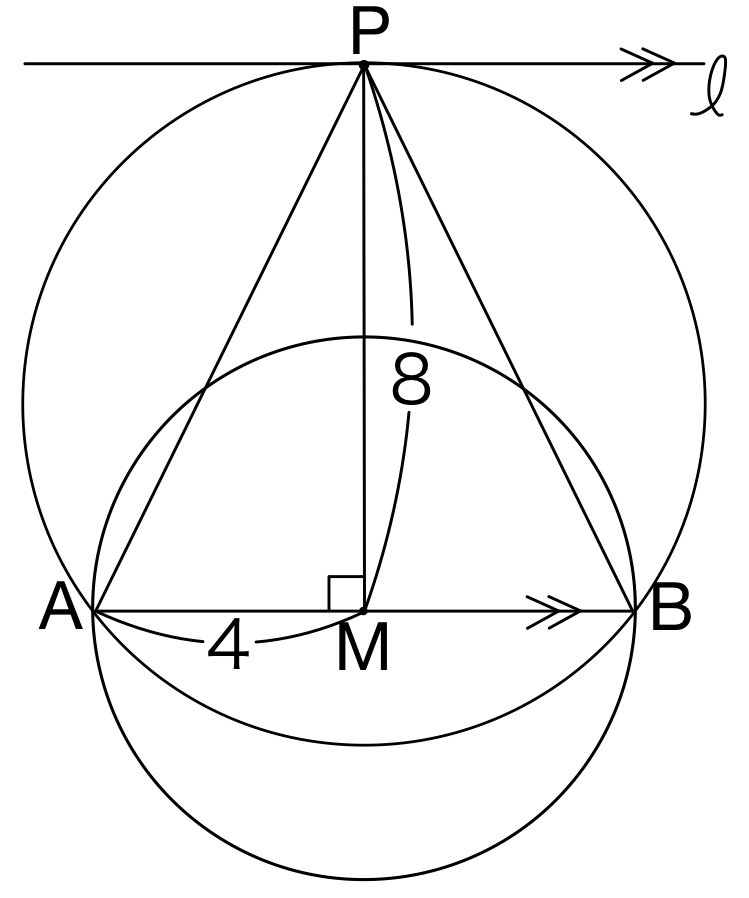\(h=8\) のとき，\(\triangle ABP\) の外接円の半径 \(R\) が最小となるのは，(２)の結果から \(AP=BP\) のときで，右図のようになる．

\(BP=AP=\sqrt{AM^2+MP^2}=\sqrt{4^2+8^2}=4\sqrt{5}\)

である．

\(\triangle ABP\) で余弦定理より

\(\cos \angle APB=\displaystyle\frac{\left(4\sqrt{5}\right)^2+\left(4\sqrt{5}\right)^2-8^2}{2\cdot 4\sqrt{5}\cdot 4\sqrt{5}}=\displaystyle\frac{3}{5}\)

また，\(0°< \angle APB<180°\) より \(\sin \angle APB>0\) であるから

\(\sin \angle APB=\sqrt{1-\cos^2 \angle APB}=\displaystyle\frac{4}{5}\) ・・・《チツ》

このとき，正弦定理から

\(2R=\displaystyle\frac{AB}{\sin\angle APB}=\displaystyle\frac{8}{\displaystyle\frac{4}{5}}\)

したがって，\(R=5\) ・・・《テ》