 2021年入試問題
2021年入試問題 【2021早稲田大学・教育】共有点をもつ共通接線(数学Ⅲ)
指数関数と2次関数が共有点をもち、共通接線をもつ。接点のx座標をpとおき、y座標の一致、接線の傾き(x=pにおける微分係数)の一致から考える。数学Ⅲ:微分。頻出・重要問題。
 2021年入試問題
2021年入試問題 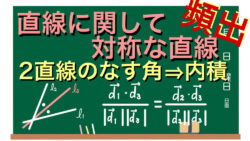 ベクトル
ベクトル  2022年入試問題
2022年入試問題  2021年入試問題
2021年入試問題  極限
極限  微分・積分(数学Ⅲ)
微分・積分(数学Ⅲ)  極限
極限  極限
極限  京都大学
京都大学  京都大学
京都大学  微分・積分(数学Ⅲ)
微分・積分(数学Ⅲ)  積分まとめ
積分まとめ  図形と方程式
図形と方程式  京都大学
京都大学  京都大学
京都大学  場合の数・確率
場合の数・確率  数列
数列  三角関数
三角関数  図形と方程式
図形と方程式  数学(大学入試問題)
数学(大学入試問題)  式と証明
式と証明  2022年入試問題
2022年入試問題  積分まとめ
積分まとめ  共通テスト(センター試験)
共通テスト(センター試験)