【2009京都大学・甲・第６問】
極方程式 \(r=1+\cos \theta\) ( \(0≦\theta≦\pi\) ) で表される曲線の長さを求めよ．
極座標と極方程式
極座標
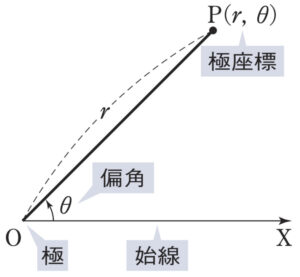平面上に点 \(O\) と半直線 \(OX\) を定めると，この平面上の任意の点 \(P\) の位置は，\(OP\) の長さ \(r\) と，\(OX\) から半直線 \(OP\) へ測った角 \(\theta\) で決まる．
このとき，\(2\) つの数の組 \((r,\theta)\) を点 \(P\) の 極座標 といい，定点 \(O\) を極，半直線 \(OX\) を始線，角 \(\theta\) を偏角という．
※ 極 \(O\) の極座標は，任意の数 \(\theta\) を用いて \(0,\theta\) と定める．また，\(\theta\) は弧度法で表した一般角．
極座標と直交座標の関係
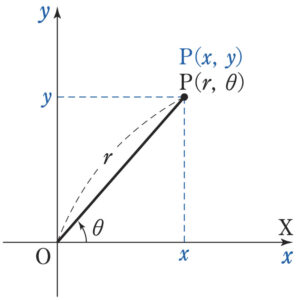極座標に対して，これまで用いてきた \(x\) 座標，\(y\) 座標の組 \((x,y)\) で表した座標を直交座標という．
座標平面において，極座標を考えるとき，原点 \(O\) を極，\(x\) 軸の正の部分を始線とすると，極座標と直交座標の間には次の関係がある．
１．\(x=r\cos \theta\) , \(y=r\sin \theta\)
２．\(r=\sqrt{x^2+y^2}\)
極方程式
ある曲線が極座標 \((r, \theta)\) に関する方程式 \(r=f(\theta)\) や \(F(r, \theta)=0\) で表されるとき，この方程式を曲線の 極方程式 という．
曲線の長さ
京都大学では、2002年、2021年にも曲線の長さが出題されています！
しっかりと対策を！
媒介変数された曲線の長さ
曲線 \(x=f(t)\) , \(y=g(t)\) ( \(\alpha≦t≦\beta\) ) の長さ \(L\) は
\(L=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left(\displaystyle\frac{dx}{dt}\right)^2+\left(\displaystyle\frac{dy}{dt}\right)^2} dt=\displaystyle\int^{\beta}_{\alpha}\sqrt{\left\{f^{\prime}(t)\right\}^2+\left\{g^{\prime}(t)\right\}^2} dt\)
曲線 \(y=f(x)\) の長さ
曲線 \(y=f(x)\) ( \(a≦x≦b\) ) の長さ \(L\) は
\(L=\displaystyle\int^{b}_{a}\sqrt{1+\left(\displaystyle\frac{dy}{dx}\right)^2} dx=\displaystyle\int^{b}_{a}\sqrt{1+\left\{f^{\prime}(x)\right\}^2} dx\)
解答・解説
【2009京都大学・甲・第６問】
極方程式 \(r=1+\cos \theta\) ( \(0≦\theta≦\pi\) ) で表される曲線の長さを求めよ．
\(r=1+\cos \theta\) より曲線の媒介変数表示は
\(\begin{cases}x=r\cos \theta=(1+\cos \theta)\cos \theta\\y=r\sin \theta=(1+\cos \theta)\sin \theta \end{cases}\)
であるから，
\(\displaystyle\frac{dx}{d\theta}=-\sin \theta\cos \theta+(1+\cos \theta)(-\sin \theta)\)
\(=-\sin \theta-2\sin \theta\cos \theta=-\sin \theta-\sin 2\theta\)
\(\displaystyle\frac{dy}{d\theta}=-\sin^2 \theta+(1+\cos \theta)\cos \theta\)
\(=\cos \theta+\cos^2 \theta-\sin^2 \theta=\cos \theta+\cos 2\theta\)
ゆえに，
\(\left(\displaystyle\frac{dx}{d\theta}\right)^2+\left(\displaystyle\frac{dy}{d\theta}\right)^2\)
\(=(-\sin \theta-\sin 2\theta)^2+(\cos \theta+\cos 2\theta)^2\)
\(=2+2(\sin \theta\sin 2\theta+\cos \theta\cos 2\theta)\)
\(=2+2\cos(2\theta-\theta)\)
\(=2(1+\cos \theta)\)
\(=4\cos^2 \displaystyle\frac{\theta}{2}\)
よって，求める曲線の長さ \(L\) は
\(L=\displaystyle\int^{\pi}_{0}\sqrt{\left(\displaystyle\frac{dx}{d\theta}\right)^2+\left(\displaystyle\frac{dy}{d\theta}\right)^2} d\theta\)
\(=\displaystyle\int^{\pi}_{0}\sqrt{4\cos^2 \displaystyle\frac{\theta}{2}} d\theta\)
\(0≦\theta≦\pi\) より \(\cos\displaystyle\frac{\theta}{2}≧0\) なので
\(L=\displaystyle\int^{\pi}_{0}\cos \displaystyle\frac{\theta}{2}d\theta\)
\(=\Bigl[4\sin \displaystyle\frac{\theta}{2}\Bigr]^{\pi}_{0}=4\)
コメント