【2007京都大学】
座標空間で点 \( ( 3 , 4 , 0 )\) を通り,ベクトル \(\overrightarrow{a}=( 1 , 1 , 1 )\) に平行な直線を \(l\) , 点 \( ( 2 , -1 , 0 )\) を通り,ベクトル \(\overrightarrow{b}=( 1 , -2 , 0 )\) に平行な直線を \(m\) とする.点 \(P\) は直線を \(l\) 上 , 点 \(Q\) 直線を \(m\) 上をそれぞれ勝手に動くとき,線分 \(PQ\) の長さの最小値を求めよ.
空間の直線の方程式(媒介変数表示)

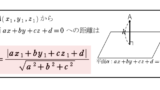
その他,空間の平面の方程式や点と面の距離の公式など,難関大学では頻出テーマ(※特に京都大学では頻出)になります。演習問題や公式のまとめは「平面の方程式・点と平面の距離・空間上の直線の方程式・外積の公式まとめ・例題演習」を参考にしてください。
【解答】媒介変数表示
実数 \(s\) , \(t\) を用いて,
\(\overrightarrow{OP}=( 3 , 4 , 0 )+s\overrightarrow{a}=(s+3,s+4,s)\)
\(\overrightarrow{OQ}=( 2 , -1 , 0 )+t\overrightarrow{b}=(t+2,-2t-1,0)\)
とおくことができる.

このように, \(s\) , \(t\) を用いて点 \(P\) や \(Q\) を表すことを,媒介変数表示と言います。
\(\overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}=(-s+t-1,-s-2t-5,-s)\) ・・・①
( ⅰ ) 予選決勝法(1文字固定)
①より,
\(\left|\overrightarrow{PQ}\right|^2=(-s+t-1)^2+(-s-2t-5)^2+(-s)^2\)
\(=3s^2+2st+5t^2+12s+18t+26\)

\(s\) , \(t\) の \(2\) 変数関数の式の最小値の問題になった!
予選決勝法(\(1\) 文字固定)が使えるパターンです!
※\(2\) 変数関数の最大・最小値の求め方については,「2変数関数の最大値・最小値【1文字固定法(予選決勝法)】」で詳しく説明をしています。参考にしてください。
\(s\) について整理すると,
\(\left|\overrightarrow{PQ}\right|^2=3s^2+2(t+6)s+5t^2+18t+26\)
\(=3\left(s+\displaystyle\frac{t+6}{3}\right)^2+\displaystyle\frac{14}{3}t^2+14t+14\)
であるから,\(s=-\displaystyle\frac{t+6}{3}\) のとき
\(\displaystyle\frac{14}{3}t^2+14t+14=\displaystyle\frac{14}{3}\left(t+\displaystyle\frac{3}{2}\right)^2+\displaystyle\frac{7}{2}\) であるから,
\(s=-\displaystyle\frac{t+6}{3}\) かつ \(t=-\displaystyle\frac{3}{2}\) で,\(\left|\overrightarrow{PQ}\right|^2\) は最小値:\(\displaystyle\frac{7}{2}\)
したがって,\(s=t=-\displaystyle\frac{3}{2}\) のとき,
\(PQ\) の最小値は\(\sqrt{\displaystyle\frac{7}{2}}=\displaystyle\frac{\sqrt{14}}{2}\)
( ⅱ ) ベクトルの内積の利用

上の【解答】媒介変数表示の
\(\overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}=(-s+t-1,-s-2t-5,-s)\) ・・・①
までは同様です.それ以降の別解を紹介します。
\(PQ\) の長さが最小となるのは,\(PQ \perp l\) かつ \(PQ \perp m\) のときであるから,
・\(PQ \perp l\) のとき
\(\overrightarrow{PQ}\cdot\overrightarrow{a}=0\) より
\(\overrightarrow{PQ}=(-s+t-1,-s-2t-5,-s)\) , \(\overrightarrow{a}=( 1 , 1 , 1 )\) であるから,
\(\overrightarrow{PQ}\cdot\overrightarrow{a}=(-s+t-1)+(-s-2t-5)+(-s)=0\)
よって, \(3s+t+6=0\) ・・・②
・\(PQ \perp m\) のとき
\(\overrightarrow{PQ}\cdot\overrightarrow{b}=0\) より
\(\overrightarrow{PQ}=(-s+t-1,-s-2t-5,-s)\) , \(\overrightarrow{b}=( 1 , -2 , 0 )\) であるから,
\(\overrightarrow{PQ}\cdot\overrightarrow{b}=(-s+t-1)-2(-s-2t-5)=0\)
よって, \(s+5t+9=0\) ・・・③
②,③より,\(s=t=-\displaystyle\frac{3}{2}\)
このとき,\(\overrightarrow{PQ}=\left(-1,-\displaystyle\frac{1}{2},\displaystyle\frac{3}{2}\right)\) より
線分 \(PQ\) の最小値は,\(\sqrt{(-1)^2+\left(-\displaystyle\frac{1}{2}\right)^2+\left(\displaystyle\frac{3}{2}\right)^2}=\displaystyle\frac{\sqrt{14}}{2}\)








コメント