【2015東京大学】曲線の通過領域｜パラメータ(媒介変数)aの存在条件・２次方程式の実数解の存在条件

通過領域について

通過領域の問題は入試頻出です！

今までに経験したことがない人は，「【頻出】通過領域・逆像法(逆手流)《考え方》」をまず確認しましょう！

【頻出】通過領域・逆像法(逆手流)《考え方》

大学入試で重要かつ頻出分野。数学Ⅱ（図形と方程式）の通過領域の解法（考え方・思考の仕方）について具体的に実験を通して解説。実数存在条件。1文字固定法。

mathmathmanabu.com

2021.08.05

基本的な通過領域の問題をしっかりとマスターした上で東大の問題にチャレンジしましょう！

方針・考え方

$y=ax^2+\displaystyle\frac{1-4a^2}{4a}$ を $a$ の $2$ 次方程式と考える

$4(x^2-1)a^2-4ya+1=0$ ・・・①

①の $a$ の 方程式が正の実数解を少なくとも $1$ つもてばよい

ここで，$f(a)=4(x^2-1)a^2-4ya+1$ は

• $x^2-1<0$ のとき上に凸の放物線
• $x^2-1=0$ のとき直線
• $x^2-1>0$ のとき下に凸の放物線

であるから，それぞれで場合分けをして考える．

また，$f(0)=1>0$ ( $y$ 切片が正 ) であることに注目しましょう！

解答・解説

$y=ax^2+\displaystyle\frac{1-4a^2}{4a}$ より

$4(x^2-1)a^2-4ya+1=0$ ・・・①

①を $a$ の 方程式と考えて，正の範囲に少なくとも $1$ つの実数解をもつ条件を考えればよい．

ここで，$f(a)=4(x^2-1)a^2-4ya+1$ とおく．

$f(0)=1>0$ であることに注意して以下考える．

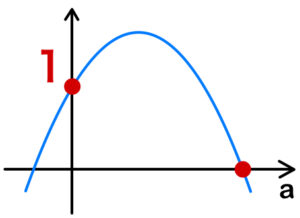( ⅰ )　$x^2-1<0$ $\iff$ $-1<x<1$ のとき

$f(a)=4(x^2-1)a^2-4ya+1$ は上に凸の放物線で，

$f(0)=1>0$ であるから，①は $y$ の値によらず $a$ が正の範囲において実数解をもつ．

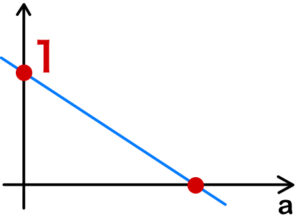( ⅱ )　$x^2-1=0$ $\iff$ $x=\pm1$ のとき

$f(a)=-4ya+1$ は直線で，$f(0)=1>0$ であるから

傾き $-4y<0$ となればよい．

よって，$y>0$

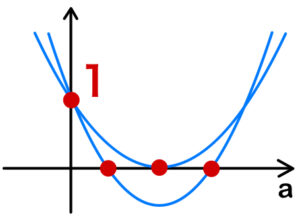( ⅲ )　$x^2-1>0$ $\iff$ $x<-1 , 1<x$ のとき

$f(a)=4(x^2-1)a^2-4ya+1$ は下に凸の放物線で，$f(0)=1>0$ でるから，

軸 ：$a=\displaystyle\frac{4y}{2\cdot4(x^2-1)}>0$ かつ

$f(a)=0$ の判別式 $D$ が $D≧0$ を満たせばよい．

2次方程式が正の範囲に解をもつ条件の考え方については，

解の配置(分離)の問題を確認してください！

【頻出】２次関数の解の配置(分離)：１より大きい異なる２つの解、異符号の解など２パターン完全マスター

軸 ：$a=\displaystyle\frac{4y}{2\cdot4(x^2-1)}>0$ より

$x^2-1>0$ であるから $y>0$

また，$\displaystyle\frac{D}{4}=4y^2-4(x^2-1)≧0$

よって，$x^2-y^2≦1$

( ⅰ )〜( ⅲ )より

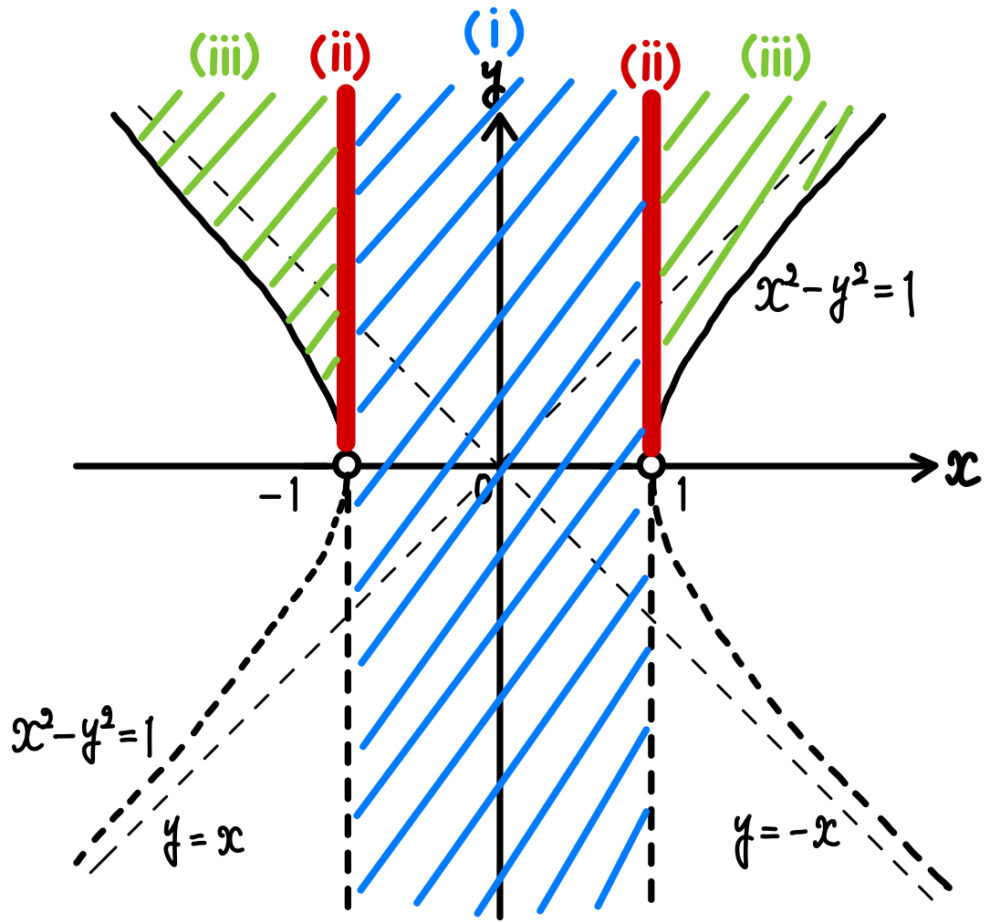
ただし境界線は実線部分を含み，点線部分は含まない．