2021 学習院大学・理学部｜ある範囲で\(f(x)>0\)を満たす条件［２次不等式］

考え方・Point

(※厳密には最小値でなく下限)

そもそも不等式とは、両辺のグラフの上下関係を表した式である．

つまり、\(f(x)≧0\) が成り立つと言うことは、

\(y=f(x)\) のグラフが、\(y=0\) ( \(x\) 軸 ) より上側(または接する)

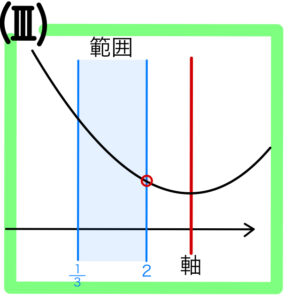
視覚的には下図のようなイメージ

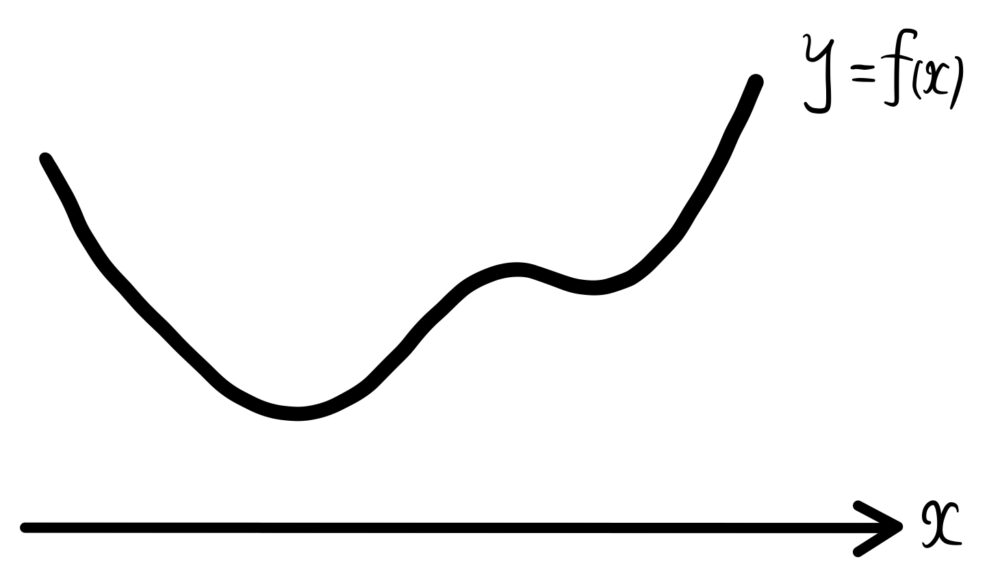
この図の状況を満たすためには、(\(f(x)\) の最小値) \(≧0\)

であれば、\(y=f(x)\) のグラフは \(y=0\) ( \(x\) 軸 ) より上側(または接する)にあり、条件を満たすことが出来る。

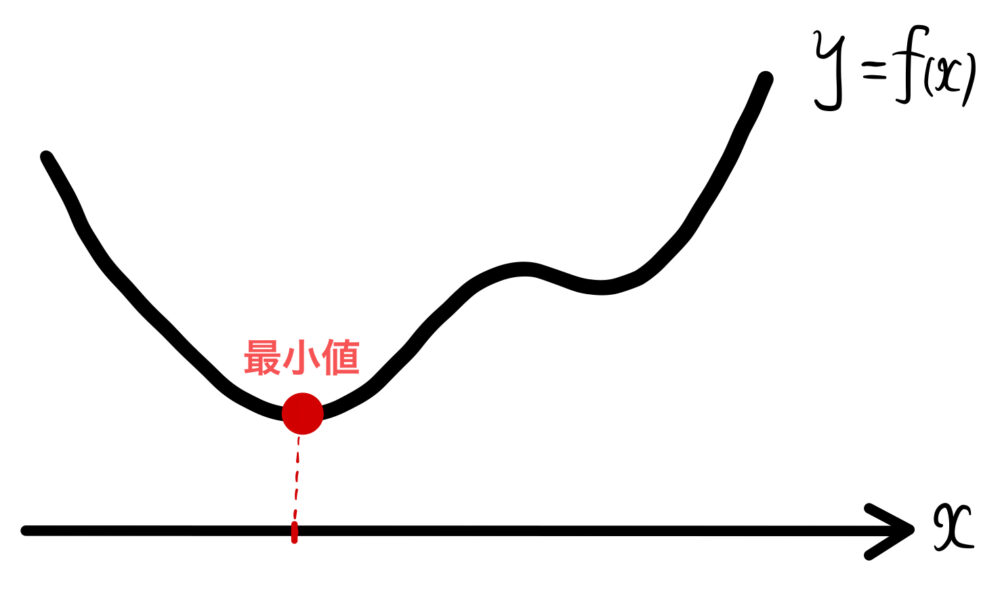
※ざっくり言うと、一番低いところが浮いていたら、残りのグラフも浮いている

解答の流れ・指針

\(f(x)=3x^2-ax+1\) とおくとき、

\(\displaystyle\frac{1}{3}<x<2\) の範囲でのグラフが一番低いところが \(x\) 軸よりも上側にあることが言えればよい

つまり、軸が動く \(2\) 次関数の最小値の問題を基準として考えればよい

(ⅰ)　\(軸<\displaystyle\frac{1}{3}\) のとき

\(f\left(\displaystyle\frac{1}{3}\right)>0\) を満たせばよい

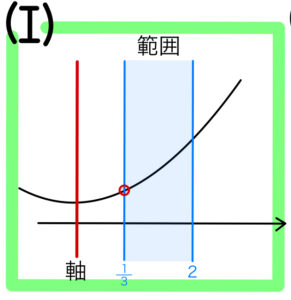
(ⅱ)　\(\displaystyle\frac{1}{3}≦軸≦2\) のとき

\(f\left(軸\right)>0\) を満たせばよい

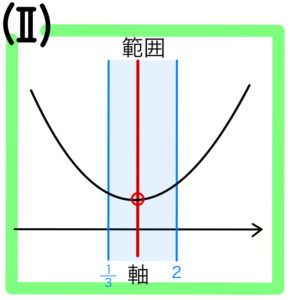
(ⅲ)　\(2<軸 \) のとき

\(f(2)>0\) を満たせばよい

解答

\(f(x)=3x^2-ax+1\) とおく．

\(f(x)=3\left(x-\displaystyle\frac{a}{6} \right)^2-\displaystyle\frac{a^2}{12}+1\)

(ⅰ)　\(\displaystyle\frac{a}{6}<\displaystyle\frac{1}{3} \iff a<2\) のとき

\(f\left(\displaystyle\frac{1}{3}\right)=\displaystyle\frac{1}{3}-\displaystyle\frac{a}{3}+1>0\)

よって、\(a<4\)

\(a<2\) と共通部分を考えて、\(a<2\) ・・・ ①

(ⅱ)　\(\displaystyle\frac{1}{3}≦\displaystyle\frac{a}{6}≦2 \iff 2≦a≦12\) のとき

\(f\left(\displaystyle\frac{a}{6}\right)=-\displaystyle\frac{a^2}{12}+1>0\)

よって、\(-2\sqrt{3}<a<2\sqrt{3}\)

\(2≦a≦12\) と共通部分を考えて、\(2≦a<2\sqrt{3}\) ・・・ ②

(ⅲ)　\(2<\displaystyle\frac{a}{6} \iff 12<a\) のとき

\(f(2)=12-2a+1>0\)

よって、\(a<\displaystyle\frac {13}{2}\)

\(12<a\) より不適

①、②より、\(a<2\sqrt{3}\)