【2021札幌医科大】
体積が \(\displaystyle\frac{\sqrt{2}}{3}\pi\) の直円錐において,直円錐の側面積の最小値を求めよ.ただし直円錐とは,底面の円の中心と頂点とを結ぶ直線が,底面に垂直である円錐のことである.
解答・解説
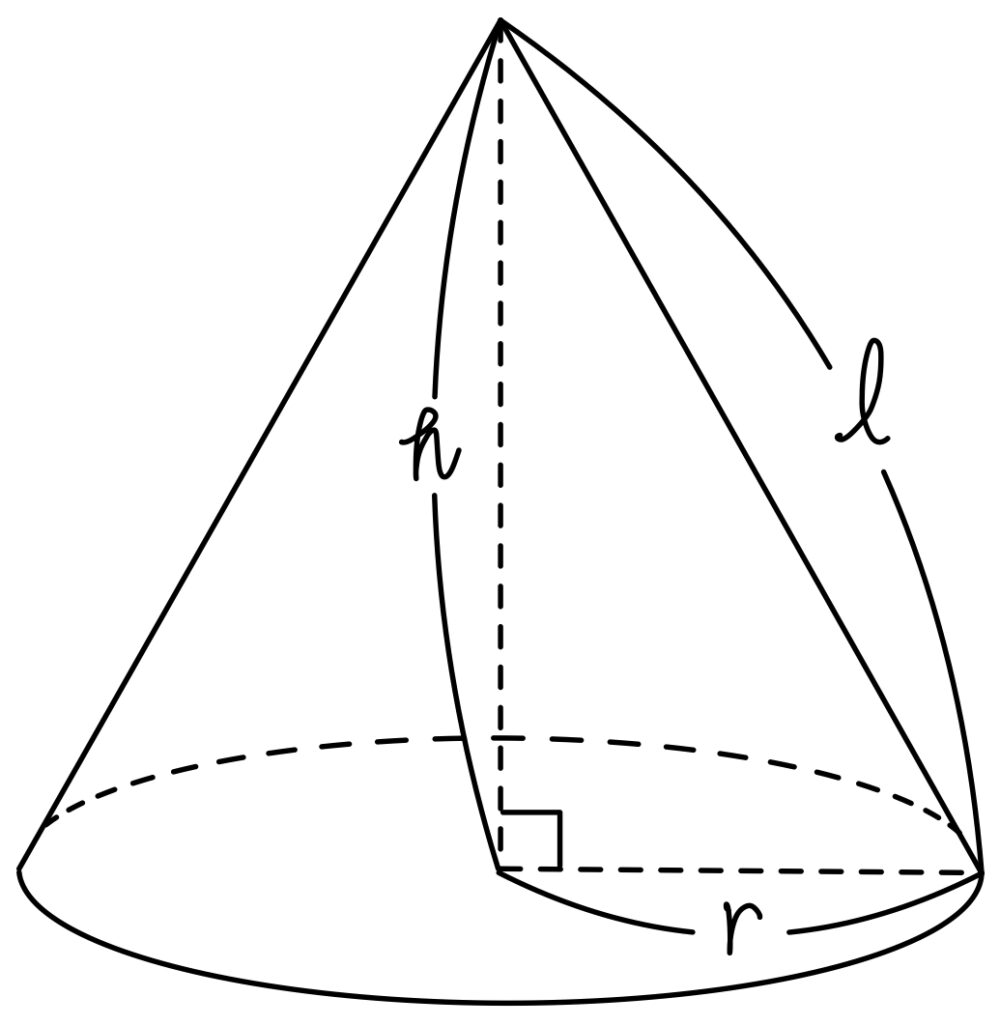 直円錐の底面の円の半径を \(r\) ,高さを \(h\) ,母線の長さを \(l\) とおくと,
直円錐の底面の円の半径を \(r\) ,高さを \(h\) ,母線の長さを \(l\) とおくと,
\(l=\sqrt{r^2+h^2}\) ,\(r>0\) ,\(h>0\) ・・・①
体積が \(\displaystyle\frac{\sqrt{2}}{3}\pi\) であるから,
\(\displaystyle\frac{1}{3}\pi hr^2=\displaystyle\frac{\sqrt{2}}{3}\pi\)
よって,\(h=\displaystyle\frac{\sqrt{2}}{r^2}\) ・・・②
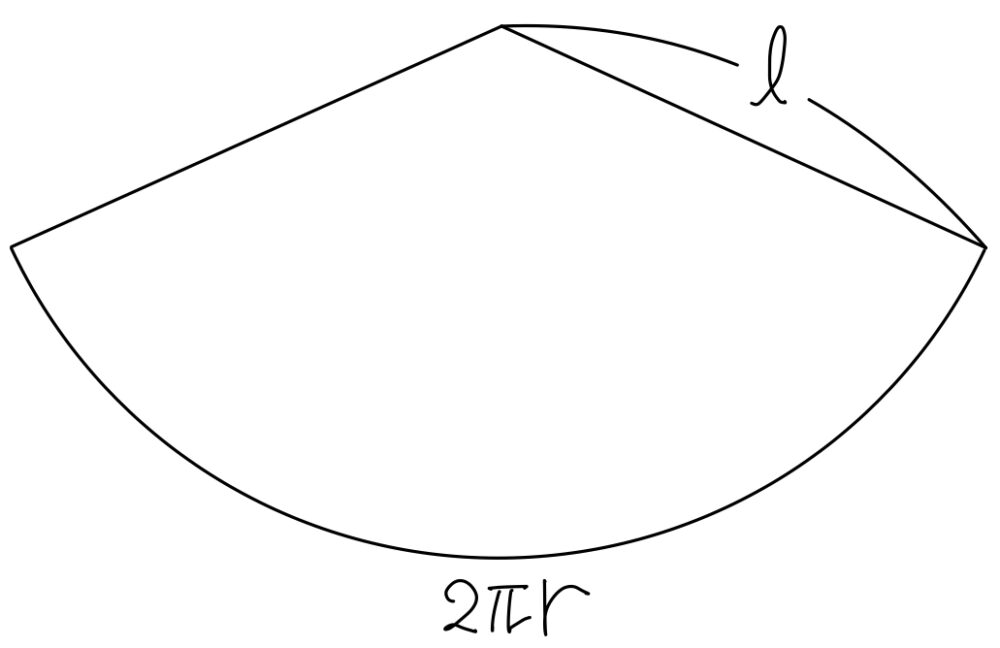 また,この直円錐の側面は右図のように扇形となるので,その面積を \(S\) とすると,
また,この直円錐の側面は右図のように扇形となるので,その面積を \(S\) とすると,
\(S=\displaystyle\frac{1}{2}\cdot l \cdot 2\pi r=\pi lr\) より
①,②の結果から
\(S=\pi r\sqrt{r^2+\displaystyle\frac{2}{r^4}}=\pi\sqrt{r^4+\displaystyle\frac{2}{r^2}}\)

\(S\) の最小値については,2通りの解法を紹介します!
いずれも使えるように!!

数学Ⅲ:微分積分を利用した解答
\(S=\pi\sqrt{r^4+\displaystyle\frac{2}{r^2}}\)

\(r\) の関数として微分してもOKですが,計算を楽にするために,置き換えをしましょう!その際に範囲の確認をお忘れなく!!
\(x=r^2\) とおく ( \(x>0\) )
\(S=\pi\sqrt{x^2+\displaystyle\frac{2}{x}}\)
ここで,\(f(x)=x^2+\displaystyle\frac{2}{x}\) とおく.
\(f^{\prime}(x)=2x-\displaystyle\frac{2}{x^2}=\displaystyle\frac{2(x-1)(x^2+x+1)}{x^2}\)
\(f^{\prime}(x)=0\) のとき \(x=1\)
| \(x\) | \(0\) | ・・・ | \(1\) | ・・・ |
| \(f^{\prime}(x)\) | ー | \(0\) | + | |
| \(f(x)\) | ↘️ | \(3\) | ↗️ |
したがって,\(f(x)\) は \(x=1\) で最小値 \(3\) をとる.
よって,直円錐の側面積 \(S\) の最小値は \(\sqrt{3}\pi\)
数学Ⅱ:相加平均・相乗平均を利用した解答
\(3\) つの相加平均・相乗平均の関係
\(a≧0\)、\(b≧0\)、\(c≧0\) のとき
\(\displaystyle\frac{a+b+c}{3}≧\sqrt[3]{abc}\)
等号成立は \(a=b=c\) のとき
\(S=\pi\sqrt{r^4+\displaystyle\frac{2}{r^2}}=r^4+\displaystyle\frac{1}{r^2}+\displaystyle\frac{1}{r^2}\)
\(r>0\) より相加平均・相乗平均の関係から,
\(r^4+\displaystyle\frac{1}{r^2}+\displaystyle\frac{1}{r^2}≧3\sqrt[3]{r^4\times \displaystyle\frac{1}{r^2}\times \displaystyle\frac{1}{r^2}}=3\)
(等号成立は \(r=1\) のとき )
よって \(r^4+\displaystyle\frac{2}{r^2}\) は最小値 \(3\) をとるので,
したがって,求める \(S\) の最小値は \(\sqrt{3}\pi\)







コメント