【2021 大阪市立大学 文系[第3問]】

はじめに
2021年の大阪市立大学・文系の問題です。
2021年の大阪市立大学の問題は、文系の生徒にとっては非常に難しく、数学が苦手な生徒にって、非常に苦戦したようです。
実際に私の生徒も、数学で撃沈した人も・・・。
逆に、共通テストでD・E判定だった生徒が、数学で大逆転をして合格した生徒もいました。
大阪市立大学の問題は差がつく問題が非常に多く、中堅国公立を志望校とする生徒は当然、難関大学を考えている人も、良い演習になりますので、一度チャレンジしてみましょう!
2021年度の第3問は、「通過領域」に関する問題です。
通過領域の問題が初めて、考え方をちゃんと理解していない人は、
でどのように考えるのか勉強してみてください!
【解答】2021大阪市立大学
\(y=3tx^2-t^3\) より
\(t^3-3x^2t+y=0\) ・・・ ①
題意を満たすためには、
①が異なる 3 つの実数解を持てばよい.
①の左辺を \(f(t)\) とおく
\(f^{\prime}(t)=3t^2-3x^2=3(t+x)(t-x)\)
(ⅰ) \(x=0\) のとき
\(f^{\prime}(t)=3t^2>0\) より
\(y=f(t)\) は、単調増加なグラフであるから、
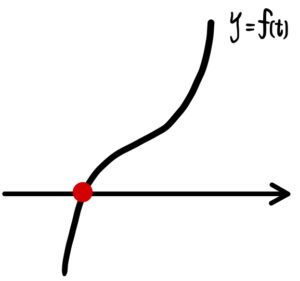
\(f(t)=0\) は 1 つしか実数解を持たない
よって不適
(ⅱ) \(x≠0\) のとき
(ア) \(x>0\) のとき
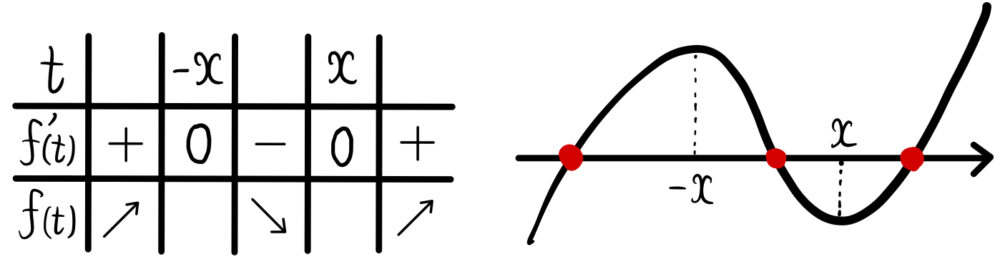
\(f(t)=0\) が異なる 3 実解を持つためには、
\(f(-x)>0\) かつ \(f(x)<0\) を満たせばよい
(イ) \(x<0\) のとき
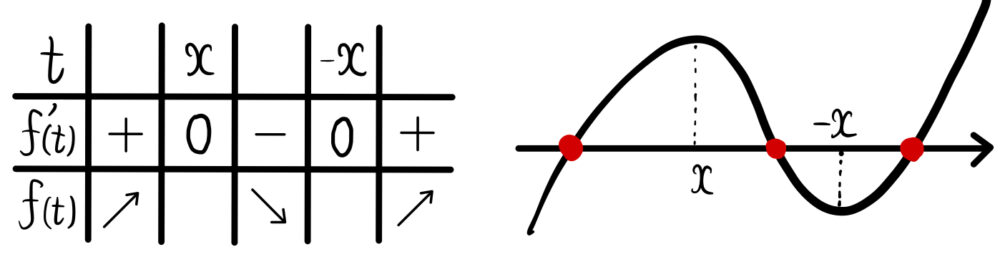
\(f(t)=0\) が異なる 3 実解を持つためには、
\(f(-x)<0\) かつ \(f(x)>0\) を満たせばよい
\(f(-x)=2x^3+y\)、\(f(x)=-2x^3+y\) より
(ア) \(x>0\) のとき
\(f(-x)=2x^3+y>0\)
\(f(x)=-2x^3+y<0\)
つまり、
\(\begin{cases}x>0\\y>-2x^3\\y<2x^3 \end{cases}\)
(イ) \(x<0\) のとき
\(f(-x)=2x^3+y<0\)
\(f(x)=-2x^3+y>0\)
つまり、
\(\begin{cases}x<0\\y<-2x^3\\y>2x^3 \end{cases}\)
それぞれ図示すると、
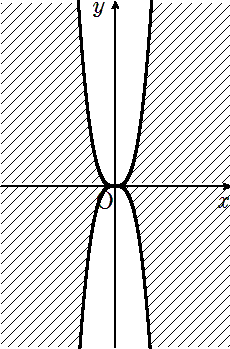
したがって求める領域は、上の斜線部.
ただし、境界線は含まない.
最後に
いかがだったでしょうか?
受験数学ではオーソドックスな問題ではありますが、しっかりと経験したことがないと、なかなか手が出ない問題かもしれません。
しっかりと有名パターンの問題にはしっかり触れておく必要があるため、網羅性が強い問題集として、「標準問題精講」などの問題集をしっかりと仕上げておきましょう!








コメント