【2023福岡大学・医学部】
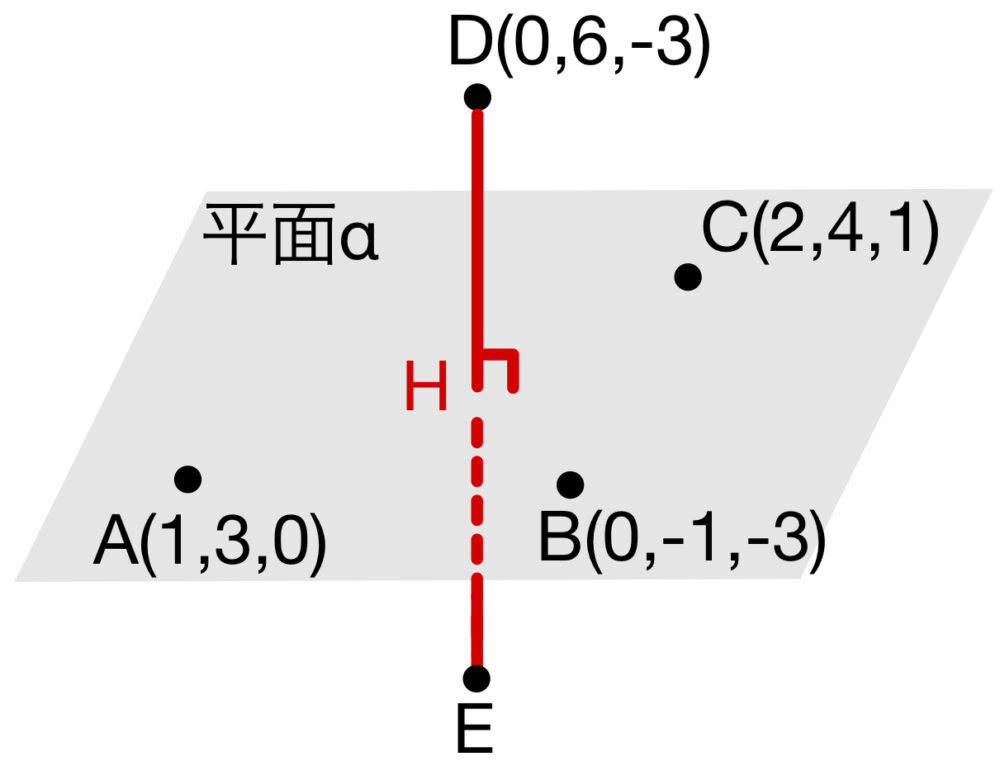
座標空間において,\(3\) 点 \(A(1,3,0)\),\(B(0,-1,-3)\),\(C(2,4,1)\) が定める平面を \(\alpha\) とし,\(D(0,6,-3)\) とする.このとき,\(\alpha\) に関して \(D\) と対称な点 \(E\) の座標は [ ] である.ただし,\(E\) が \(\alpha\) に関して \(D\) と対称であるとは,直線 \(DE\) は \(\alpha\) に垂直であり,かつ線分 \(DE\) の中点は \(\alpha\) 上にあることをいう.また,\(F(1,1,1)\) とするとき,\(\alpha\) 上の点 \(P\) で,\(2\) 線分 \(DP\),\(FP\) の長さの和 \(DP+FP\) を最小にする \(P\) の座標は [ ] である.

平面の方程式,点と面の距離の公式,外積など,学校の授業では学習しないけど,入試では頻出の知っておきたい差がつくテーマになります。
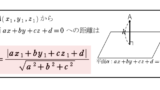
(前半)考え方・方針について
外積について
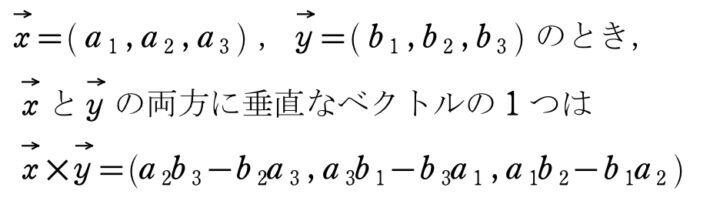
※ \(\vec{x}\times\vec{y}\) を \(\vec{x}\) と \(\vec{y}\) の外積という
※ 外積は高校数学では学習しません。(教科書に載っていません)そのため,記述式の答案で使用すると、減点される可能性があります。使用する場合は、記述として解答に残さないこと!
平面の方程式について
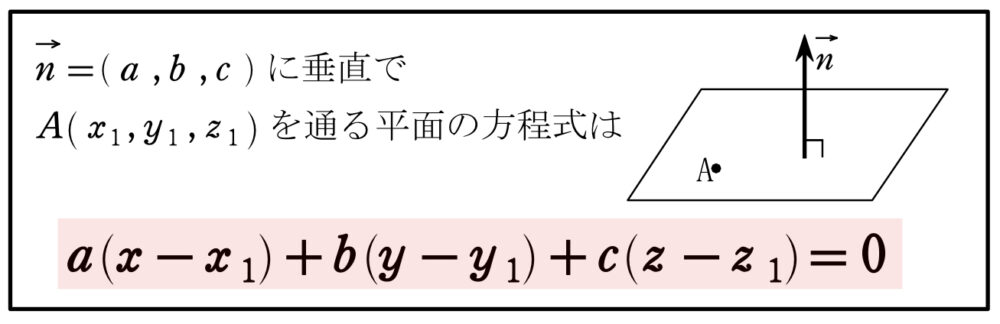
知らなくても解けますが,知っておくと色々と便利で計算が簡略化できます!
特に難関大学では頻出ですので,覚え・使えるように!


(前半)解答・解説
\(\overrightarrow{AB}=(-1,-4,-3)\),\(\overrightarrow{AC}=(1,1,1)\) より,\(\overrightarrow{AB}\) と \(\overrightarrow{AC}\) の両方に垂直なベクトルの \(1\) つを \(\overrightarrow{n}\) とおくと
\(\overrightarrow{n}=(-1,-2,3)\) となる.
よって平面 \(\alpha\) の方程式は
\(-(x-1)-2(y-3)+3(z-0)=0\)
\(\iff\) \(x+2y-3z-7=0\) ・・・①
点 \(D\) から平面 \(\alpha\) に下ろした垂線の足を \(H\) とおくと
\(DH \perp \)(平面 \(\alpha\)) より実数 \(t\) を用いて
\(\overrightarrow{OH}=\overrightarrow{OD}+\overrightarrow{DH}=\overrightarrow{OD}+t\overrightarrow{n}\) より
\(\overrightarrow{OH}=(0,6,-3)+t(-1,-2,3)=(-t,-2t+6,3t-3)\)
点 \(H\) は平面 \(\alpha\) 上より①から
\(-t+2(-2t+6)-3(3t-3)-7=0\)
\(t=1\)
よって \(H(-1,4,0)\)
\(DH=HE\) より
\(\overrightarrow{OE}=\overrightarrow{OD}+2\overrightarrow{DH}=\overrightarrow{OD}+2\overrightarrow{n}\)
\(=(0,6,-3)+2(-1,-2,3)\)
\(=(-2,2,3)\)
したがって,\(E(-2,2,3)\)
(後半)考え方・方針について

平面 \(\alpha\) に対して,点 \(D\),\(F\) が同じ側にあるのか,反対側にあるのかで,\(DP+FP\) の最小値の求め方は変わってきます。
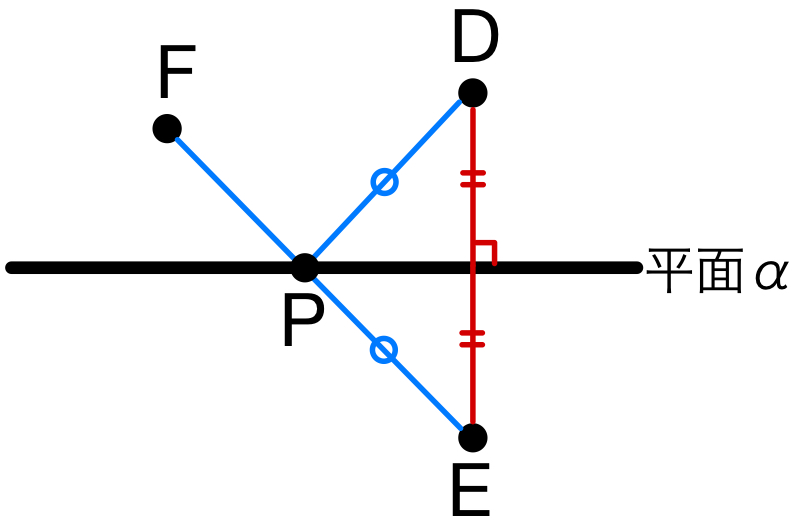 ・平面 \(\alpha\) に対して,点 \(D\),\(F\) が同じ側のとき
・平面 \(\alpha\) に対して,点 \(D\),\(F\) が同じ側のとき
平面 \(\alpha\) に関して点 \(D\) の対称点 \(E\) をとり,
直線 \(EF\) と平面 \(\alpha\) の交点を \(P\) とすると,
\(DP+FP\) は最小値をとる.
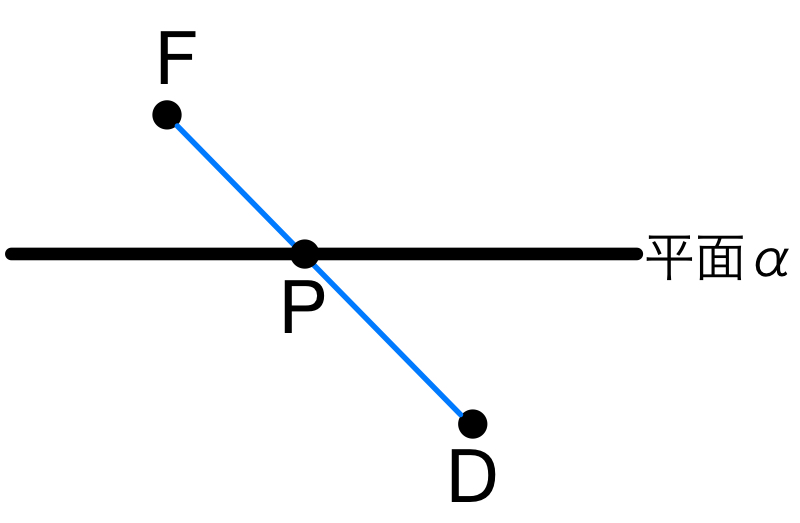 ・平面 \(\alpha\) に対して,点 \(D\),\(F\) が反対側のとき
・平面 \(\alpha\) に対して,点 \(D\),\(F\) が反対側のとき
直線 \(DF\) と平面 \(\alpha\) の交点を \(P\) とすると,
\(DP+FP\) は最小値をとる.

同じ側か、反対側にあるかはどうやって調べるの??
正確な図を書く??それともカン??

空間図形において,正確な図を書くのは非常に難しいですね。
そのような時には、「正領域・負領域」の考え方を利用しましょう!
正領域・負領域とは?
平面上の曲線 \(f(x,y)=0\) において,平面は \(2\) つに分けられる.このとき,
\(f(x,y)>0\) となる領域を正領域,\(f(x,y)<0\) となる領域を負領域 という.



(後半)解答・解説
\(f(x,y,z)=x+2y-3z-7\) とおく
点 \(D(0,6,-3)\) を代入すると
\(f(0,6,-3)=0+12+9-7>0\)
点 \(F(1,1,1)\) を代入すると
\(f(1,1,1)=1+2+3-7<0\) となり
点 \(D\),\(F\) は平面 \(\alpha\) に関して反対側にある.
よって求める \(P\) は,線分 \(DF\) と平面 \(\alpha\) の交点.
ここで実数 \(s\) を用いて,
\(\overrightarrow{OP}=\overrightarrow{OD}+s\overrightarrow{DF}\)
\(=(0,6,-3)+s(1,-5,4)\)
\(=(s,-5s+6,4s-3)\)
点 \(P\) は平面 \(\alpha\) 上より①に代入して
\(s+2(-5s+6)-3(4s-3)-7=0\)
\(s=\displaystyle\frac{2}{3}\)
したがって,\(P\left(\displaystyle\frac{2}{3},\displaystyle\frac{8}{3},-\displaystyle\frac{1}{3}\right)\)








コメント