【2023関西学院大学・全学部日程・理系・第４問】
解答・解説
(１) \(z_{3}\) および \(\alpha\) ，\(\alpha^{20}\) の値
\(z_{n+1}=\displaystyle\frac{1+i}{2}z_{n}+1\) ・・・①
\(\alpha=\displaystyle\frac{1+i}{2}\alpha+1\) ・・・② とおく．
①において \(n=1\) とすると
\(z_{2}=\displaystyle\frac{1+i}{2}z_{1}+1\)
\(z_{1}=0\) より，\(z_{2}=1\)
①において \(n=2\) とすると
\(z_{3}=\displaystyle\frac{1+i}{2}z_{2}+1\)
\(z_{2}=1\) より，\(z_{3}=\displaystyle\frac{3+i}{2}\)
②より \(2\alpha=(1+i)\alpha+2\)
\(\iff\) \((1-i)\alpha=2\)
\(\iff\) \(\alpha=\displaystyle\frac{2}{1-i}=\displaystyle\frac{2(1+i)}{(1-i)(1+i)}=\)\(1+i\)
複素数にいて，\(n\) 乗の計算は，極形式に変形してからド・モアブルの公式を使うのが一般的ですね！「【数Ⅲ】複素数平面まとめ①(絶対値について)｜入試問題演習」を参考に！
ド・モアブルの定理
\(n\) が整数のとき
\((\cos \theta+i\sin \theta)^n=\cos n\theta+i\sin n\theta\)
\(\alpha=1+i=\sqrt{2}\left(\cos\displaystyle\frac{\pi}{4}+i\sin\displaystyle\frac{\pi}{4}\right)\) より
ド・モアブルの定理から
\(\alpha^{20}=\sqrt{2}^{20}\left(\cos 5\pi+i\sin 5\pi\right)=2^{10}\times (-1)=\)\(-1024\)
(２) \(\displaystyle\sum_{n=1}^{\infty}{|z_{n}-z_{n+1}|}\) の値
①より \(z_{n+2}=\displaystyle\frac{1+i}{2}z_{n+1}+1\) ・・・③
①ー③より
\(z_{n+1}-z_{n+2}=\displaystyle\frac{1+i}{2}(z_{n}-z_{n+1})\)
\(|z_{n+1}-z_{n+2}|=\left|\displaystyle\frac{1+i}{2}\right|\cdot|z_{n}-z_{n+1}|\)
\(|z_{n+1}-z_{n+2}|=\displaystyle\frac{1}{\sqrt{2}}\cdot|z_{n}-z_{n+1}|\)
数列 \(\left\{|z_{n}-z_{n+1}|\right\}\) は，初項が \(|z_{1}-z_{2}|=1\)，公比が \(\displaystyle\frac{1}{\sqrt{2}}\) の等比数列であるから，
\(\displaystyle\sum_{n=1}^{\infty}{|z_{n}-z_{n+1}|}=\displaystyle\lim_{n\rightarrow\infty} \displaystyle\sum_{k=1}^{n}{|z_{n}-z_{n+1}|}\)
\(=\displaystyle\lim_{n\rightarrow\infty} \displaystyle\frac{1-\left(\displaystyle\frac{1}{\sqrt{2}}\right)^n}{1-\displaystyle\frac{1}{\sqrt{2}}}\)\(2+\sqrt{2}\)
(３) \(a_{n}=|z_{n}-\alpha|\) とするとき，\(a_{n}\) の一般項
①ー②より
\(z_{n+1}-\alpha=\displaystyle\frac{1+i}{2}(z_{n}-\alpha)\)
\(|z_{n+1}-\alpha|=\displaystyle\frac{1}{\sqrt{2}}(|z_{n}-\alpha|)\)
\(a_{n}=|z_{n}-\alpha|\) とおくと
\(a_{n+1}=\displaystyle\frac{1}{\sqrt{2}}a_{n}\) となり，
また\(a_{1}=|z_{1}-\alpha|=|0-(1+i)|=\sqrt{2}\)
よって，\(a_{n}=\sqrt{2}\cdot\left(\displaystyle\frac{1}{\sqrt{2}}\right)^{n-1}=\left(\displaystyle\frac{1}{\sqrt{2}}\right)^{n-2}\)
(４) \(3\) 点 \(\alpha\)，\(z_{n}\)，\(z_{n+1}\) を頂点とする三角形の面積 \(S_{n}\)
①ー②より
\(z_{n+1}-\alpha=\displaystyle\frac{1+i}{2}(z_{n}-\alpha)\)
\(a_{n}\not=0\) より \(z_{n}\not=\alpha\) であるから
\(\displaystyle\frac{z_{n+1}-\alpha}{z_{n}-\alpha}=\displaystyle\frac{1+i}{2}=\displaystyle\frac{1}{\sqrt{2}}\left(\cos\displaystyle\frac{\pi}{4}+i\sin\displaystyle\frac{\pi}{4}\right)\)
この形は，\(\alpha\) を中心とした回転移動を表していますね！
点 \(\alpha\) を中心に、点 \(\beta\) を \(k\) 倍して、角 \(\theta\) だけ回転した点が \(\gamma\) のとき
\(\gamma-\alpha=k(\cos \theta+i \sin \theta) (\beta-\alpha)\)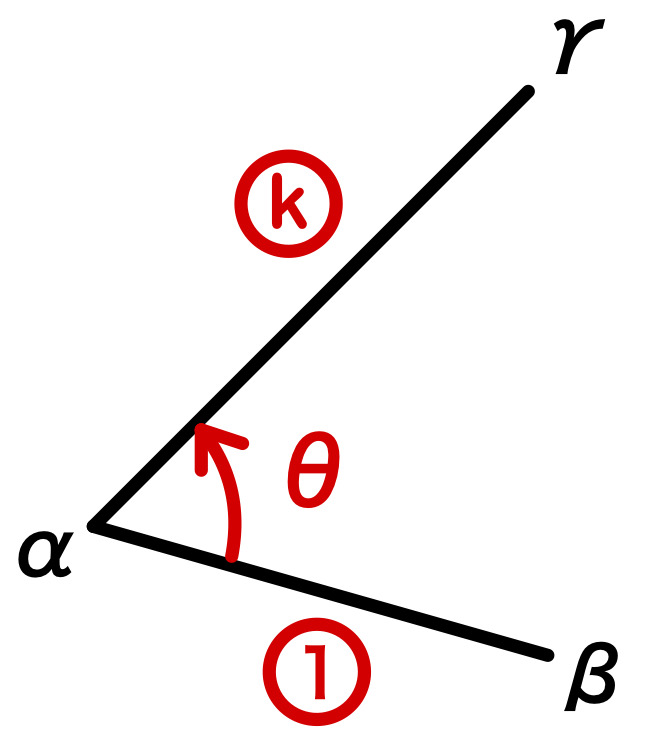
または
\(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=k(\cos \theta+i \sin \theta)\)
\(\displaystyle\frac{z_{n+1}-\alpha}{z_{n}-\alpha}=\displaystyle\frac{1}{\sqrt{2}}\left(\cos\displaystyle\frac{\pi}{4}+i\sin\displaystyle\frac{\pi}{4}\right)\) より
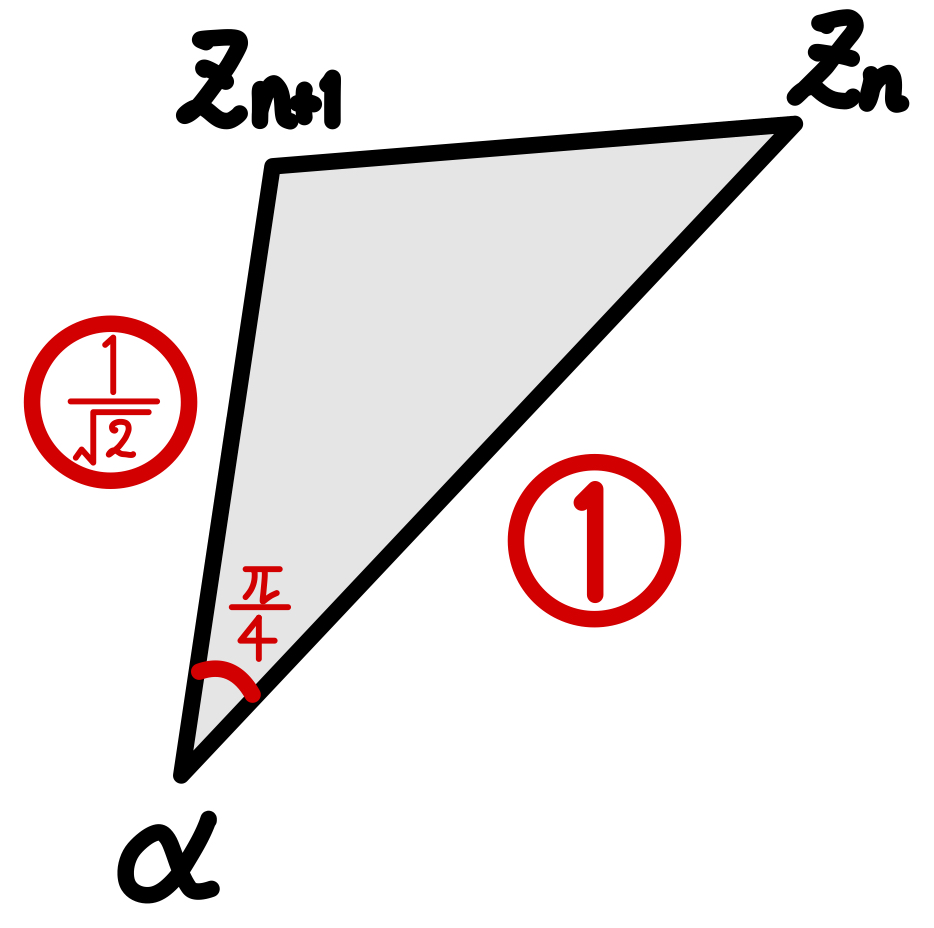点 \(\alpha\) を中心に，点 \(z_{n}\) を \(\displaystyle\frac{1}{\sqrt{2}}\) 倍して，\(\displaystyle\frac{\pi}{4}\) だけ回転した点が \(z_{n+1}\) となるので
偏角 \(arg\displaystyle\frac{z_{n+1}-\alpha}{z_{n}-\alpha}=\displaystyle\frac{\pi}{4}\)
また求める面積 \(S_{n}\) は
\(S_{n}=\displaystyle\frac{1}{2}\cdot|z_{n}-\alpha|\cdot\displaystyle\frac{1}{\sqrt{2}}|z_{n}-\alpha|\sin\displaystyle\frac{\pi}{4}\)
\(=\displaystyle\frac{1}{4}a_{n}^2=\displaystyle\frac{1}{4}\cdot\left(\displaystyle\frac{1}{2}\right)^{n-2}\)
したがって，\(S_{n}=\left(\displaystyle\frac{1}{2}\right)^n\)
コメント