【数Ⅲ】2004京都大｜複素数平面まとめ⑩(図形・方べきの定理の逆)

ここでは、数学Ⅲで学習する複素数平面について、実践問題(入試問題)を使って、ポイント(考え方)まとめをしていきます。

正直に言いますと、教科書をやっただけでは、入試レベルの問題に対応するのは難しいです。

ですから、教科書と入試レベルの橋渡しとして、過去に出題された入試問題を例に、複素数平面においておさえておきたい(入試でよく出る考え方)をまとめていきます。

基本的な考え方をしっかりと身に付け、２次試験で得点源にできるようにしていきましょう！

考え方

証明問題全般に言えること

証明問題において、方針が見えない、途中で手が止まった場合については、示したいことを言い換える(ゴールから逆算する)ことを意識しましょう！

方針・考え方

円 $C$ が $1$、$-1$ を通る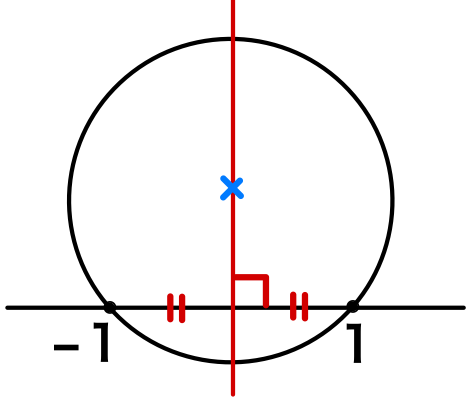

☞ $1$、$-1$ の垂直二等分線上に円 $C$ の中心がある

☞ 円 $C$ の中心は実数 $k$ を用いて、$( 0 , ki )$ とおける．

このとき、(ゴールからの逆算)

$2$ 点 $ki$ と $-\displaystyle\frac{1}{\overline{\alpha}}$ の距離が、

$2$ 点 $ki$ と $1$ の距離に等しいことが示せたら、$C$ は $-\displaystyle\frac{1}{\overline{\alpha}}$ も通ることを示すことができる．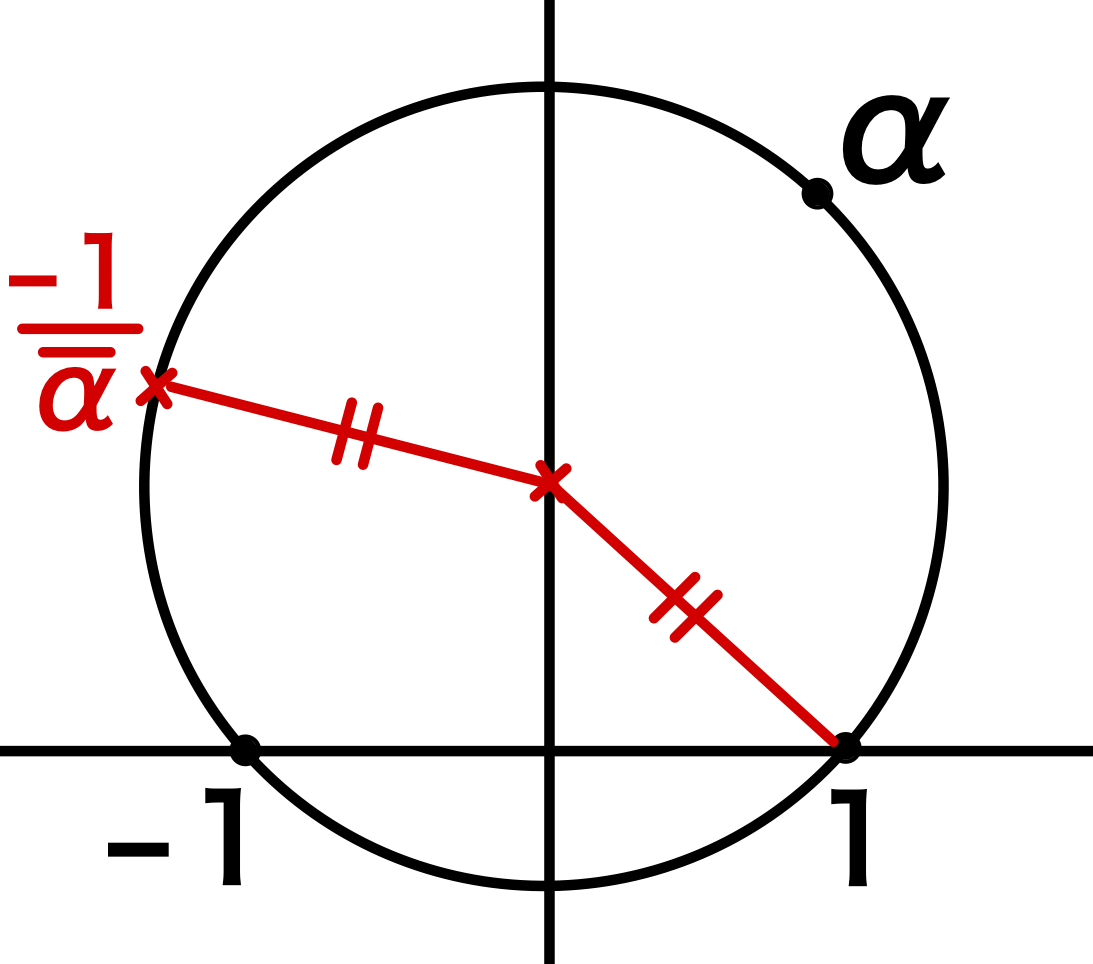

つまり、$\left| -\displaystyle\frac{1}{\overline{\alpha}}-ki \right|=| 1-ki |$ を示せばよい．

さらにゴールからの逆算を続けます。

$\left| -\displaystyle\frac{1}{\overline{\alpha}}-ki \right|^2=| 1-ki |^2$

$\iff \left(-\displaystyle\frac{1}{\overline{\alpha}}-ki\right)\left(-\displaystyle\frac{1}{\alpha}+ki\right)=(1-ki)(1+ki)$

展開して式を整理すると

$\alpha\cdot\overline{\alpha}+k\alpha i-k\overline{\alpha}i-1=0$ を示せばよい！

👆　示したいことを言い換えて、ゴールをすり替えた！

あとは問題の中で使っていない条件から、この関係式を頑張って導けばよい。

☞　まだ使っていない条件としては、$\alpha$ が円 $C$ 上にあること

解答

円 $C$ が $1$、$-1$ を通るので、円 $C$ の中心は、

$1$、$-1$ の垂直二等分線上にある．

よって、円 $C$ の中心は実数 $k$ を用いて、$( 0 , ki )$ とおける．

$C$ が $-\displaystyle\frac{1}{\overline{\alpha}}$ を通ることを示すためには、

$2$ 点 $ki$ と $-\displaystyle\frac{1}{\overline{\alpha}}$ の距離が、

$2$ 点 $ki$ と $1$ の距離に等しいことが示せればよい．

つまり、$\left| -\displaystyle\frac{1}{\overline{\alpha}}-ki \right|=| 1-ki |$ を示せばよいので、

$\left| -\displaystyle\frac{1}{\overline{\alpha}}-ki \right|^2=| 1-ki |^2$

$\iff \left(-\displaystyle\frac{1}{\overline{\alpha}}-ki\right)\left(-\displaystyle\frac{1}{\alpha}+ki\right)=(1-ki)(1+ki)$

展開して式を整理すると

$\alpha\cdot\overline{\alpha}+k\alpha i-k\overline{\alpha}i-1=0$ ・・・①を示すことが出来ればよい．

ここで、$\alpha$ は円 $C$ 上の点であるから、

$| 1-ki |=| \alpha-ki |$ より

$(1-ki)(1+ki)=(\alpha-ki)(\overline{\alpha}+ki)$

$1+k^2=\alpha\cdot\overline{\alpha}+k\alpha i-k\overline{\alpha} i+k^2$

よって、$\alpha\cdot\overline{\alpha}+k\alpha i-k\overline{\alpha} i-1=0$

したがって、①が成立するので、題意は示された．

別解

考え方：４点が同一円周上にある

別解：解答

$\alpha=| \alpha |(\cos \theta+i\sin \theta)$ とおく．

$\displaystyle\frac{1}{\alpha}=\displaystyle\frac{1}{| \alpha |}\left\{\cos (-\theta)+i\sin (-\theta)\right\}=\displaystyle\frac{1}{| \alpha |}(\cos \theta-i\sin \theta)$ なので、

$\displaystyle\frac{1}{\overline{\alpha}}=\displaystyle\frac{1}{| \alpha |}(\cos \theta+i\sin \theta)$

$-\displaystyle\frac{1}{\overline{\alpha}}=-\displaystyle\frac{1}{| \alpha |}(\cos \theta+i\sin \theta)$

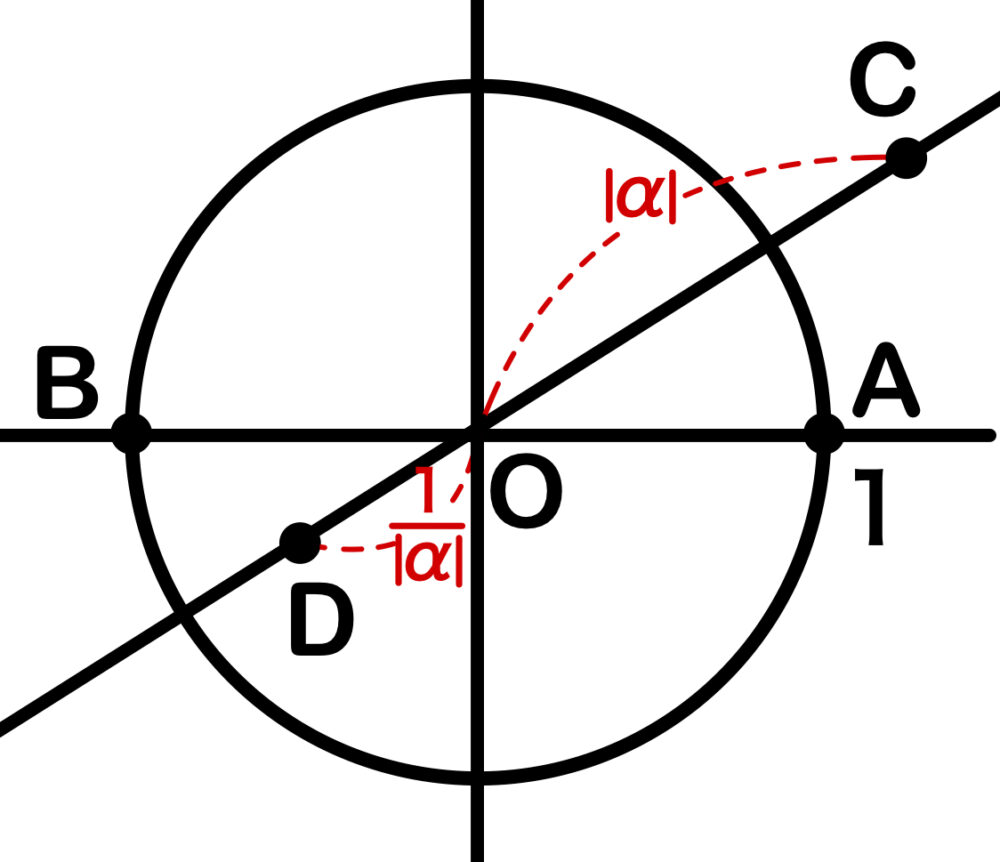
ここで、$O( 0 )$、$A ( 1 )$、$B ( -1 )$、$C (\alpha)$、$D \left(-\displaystyle\frac{1}{\overline{\alpha}}\right)$ とおく．

$OA\times OB=1\times 1=1$

$OC\times OD=| \alpha |\times \displaystyle\frac{1}{| \alpha |}=1$

よって、$OA\times OB=OC\times OD$ となり、方べきの定理の逆が成り立つので、４点 $A$、$B$、$C$、$D$ は同一円周上にある．

【数Ⅲ】複素数平面まとめ⑨(極限値・無限等比数列・三項間漸化式)｜入試問題演習

複素数の回転を利用。三項間漸化式、無限等比数列など総合問題。一橋大学過去問。 ２次試験対策。入試問題演習まとめ。様々なテーマごとに、ポイント、考え方、別解を解説。

mathmathmanabu.com

2022.01.28

【数Ⅲ】複素数平面まとめ⑪(連動型の軌跡)｜入試問題演習(2000名古屋市立大)

⑪複素数平面(数学Ⅲ)における連動型の軌跡について.2000名古屋市立大学過去問 ２次試験対策。入試問題演習まとめ。様々なテーマごとに、ポイント、考え方、別解を解説。

mathmathmanabu.com

2022.02.01