\(a\) を実数の定数とし、\(2\) つの関数
\(f(x)=x^2-4x+a+4\)、\(g(x)=-x^2-2x-2a\)
を考える.
(1) すべての実数 \(x\) に対して \(g(x)<f(x)\) が成り立つような \(a\) の値の範囲を求めよ.
(2) すべての実数 \(x_{1}\)、\(x_{2}\) に対して \(g(x_{1})<f(x_{2})\) が成り立つような \(a\) の値の範囲を求めよ.
(3) ある実数 \(x_{1}\)、\(x_{2}\) に対して \(g(x_{1})>f(x_{2})\) が成り立つような \(a\) の値の範囲を求めよ.
考え方・方針
(1)について
(1) の問題では、\(f(x)\)、\(g(x)\) ともに、共通の値 \(x\) を代入するので、下の図①のようになれば良い.逆に、下図の図①-2のような形になると、(1)の条件は満たさないことになります.
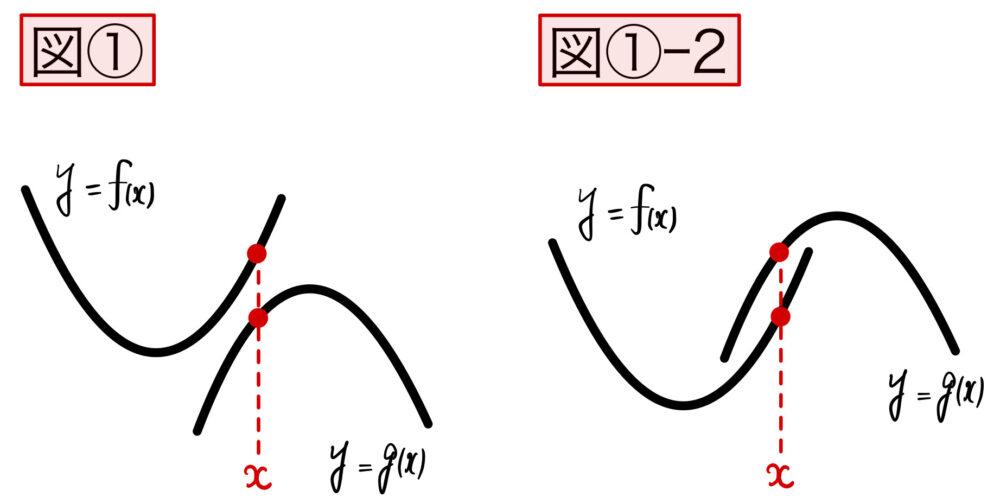
(1)の問題においては、「すべての実数 \(x\) に対して \(f(x)-(g(x)>0\) 」が成り立つ条件を考えていきます.
下記のポイントは、様々な分野で利用できますので、今回の問題に関わらず、しっかりとおさえておいて欲しいポイントです!
ある範囲において \(f(x)≧0\)
☞ (ある範囲における \(f(x)\) の最小値) \(≧0\)
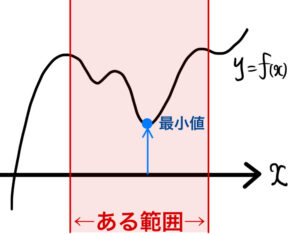
例えば上図のような \(y=f(x)\) を考える.
「ある範囲において \(f(x)≧0\)」であるとは、
「ある範囲で \(y=f(x)\) が \(x\) 軸より上側にある 」
と言う状態を表す.
「ある範囲で \(y=f(x)\) が \(x\) 軸より上側にある 」ことを言うためには、
「\(y=f(x)\) の最小値が \(x\) 軸より上側にある」ことが言えればよい.
(2)、(3)について
一方で(2)、(3)の問題では、(1)と違い、\(f(x)\)、\(g(x)\) に異なる値を代入することになります.
さらに(2)では「すべて」の値に対して、(3)では「ある」値に対してであることに注意すると、
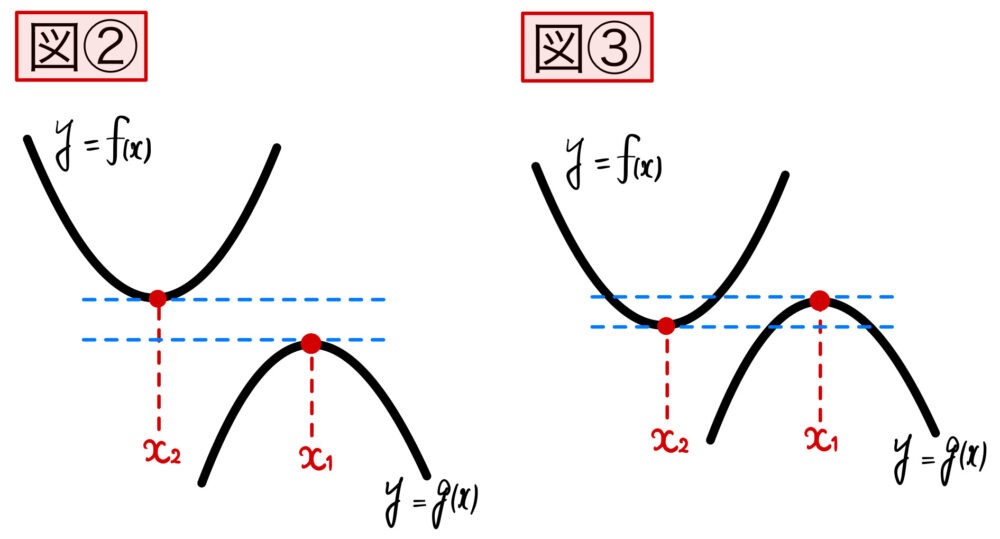
(2)は図②、(3)は図③のような状況になればよい.
それぞれの図①~③の状況を言葉で表すと、
(2)は、「 (\(g(x)\) の最大値) < (\(f(x)\) の最小値 ) 」を満たせばよい
(3)は、「 (\(g(x)\) の最大値) > (\(f(x)\) の最小値 ) 」を満たせばよい
解答
(1) 解答
\(F(x)=f(x)-g(x)\) とおく.
\(F(x)=2x^2-2x+3a+4=2\left(x-\displaystyle\frac{1}{2}\right)^2+3a+\displaystyle\frac{7}{2}\)
\(x=\displaystyle\frac{1}{2}\) で \(F(x)\) は最小値 \(3a+\displaystyle\frac{7}{2}\) をとるので、題意を満たすとき、
\(3a+\displaystyle\frac{7}{2}>0\) \(\iff a>-\displaystyle\frac{7}{6}\)
(2) 解答
「 (\(g(x)\) の最大値) < (\(f(x)\) の最小値 ) 」を満たせばよい.
\(f(x)=(x-2)^2+a\)
\(g(x)=-(x-1)^2-2a+1\) より、
\(a\) の満たす条件は、\(-2a+1<a\)
よって、\(a>\displaystyle\frac{1}{3}\)
(3) 解答
「 (\(g(x)\) の最大値) > (\(f(x)\) の最小値 ) 」を満たせばよい.
\(f(x)=(x-2)^2+a\)
\(g(x)=-(x-1)^2-2a+1\) より、
\(a\) の満たす条件は、\(-2a+1>a\)
よって、\(a<\displaystyle\frac{1}{3}\)








コメント