数学Ⅲ:積分解法手順
数学Ⅲの基本公式については,「【数学Ⅲ】積分解法手順まとめ①基本公式確認|x^a、三角・指数・対数関数、置換・部分積分」を確認しましょう!
基本公式以外の積分の問題については,以下の手順で考えていきましょう!
またそれぞれの問題においても,基本的な問題から発展的な問題まで,例題も解説しています。
Q1.三角・指数・対数関数があるか?
・NO 👉 Q2へ
・YES 👉 Q4へ
Q2.根号 ( ルート ) が入っているか?
・NO 👉 Q3へ
・YES 👉 「【数学Ⅲ】積分解法手順まとめ②根号(ルート)を含む積分」へ
Q3.分数式か?
・NO 👉 数学Ⅱの範囲の積分です!
・YES 👉 「【数学Ⅲ】積分解法手順まとめ③分数式の積分(log、部分分数分解、tan置換)」へ
Q4.三角関数が入っているか?
・NO 👉 「【数学Ⅲ】積分解法手順まとめ④指数・対数を含む積分|部分積分」へ
・YES 👉 Q5へ
Q5.三角関数のみか?
・NO 👉 「【数学Ⅲ】積分解法手順まとめ⑥(三角関数)×(多項式)の積分」へ
・YES 👉 「【数学Ⅲ】積分解法手順まとめ⑤三角関数のみの積分(置換・半角・積和・sin^nx公式)」へ
まとめ①基本公式確認|x^a、三角・指数・対数関数、置換・部分積分
次の不定積分を求めよ.
① \(\displaystyle\int \displaystyle\frac{(x\sqrt{x}-1)^2}{x}\enspace dx\)
② \(\displaystyle\int(2x+1)^3\enspace dx\)
③ \(\displaystyle\int\cos(3x+1)\enspace dx\)
④ \(\displaystyle\int e^{1-2x}\enspace dx\)
⑤ \(\displaystyle\int x\sqrt{x+1}\enspace dx\)
⑥ \(\displaystyle\int \displaystyle\sin^3 x\cos x\enspace dx\)
⑦ \(\displaystyle\int \tan x\enspace dx\)
⑧ \(\displaystyle\int \log{x}\enspace dx\)

まとめ②根号(ルート)を含む積分
① \(\displaystyle\int x\sqrt{x+1}\enspace dx\)
② \(a\) は正の定数とする.
定積分 \(\displaystyle\int^{a}_{0} \sqrt{a^2-x^2}\enspace dx\) を求めよ.
③ \(\displaystyle\int \displaystyle\frac{1}{\sqrt{x^2+1}}\enspace dx\)

まとめ③分数式の積分(log、部分分数分解、tan置換)
① \(\displaystyle\int \displaystyle\frac{2x+1}{x^2+x+1}\enspace dx\)
② \(\displaystyle\int \displaystyle\frac{x^2+3x+2}{x^2+x+1}\enspace dx\)
③ \(\displaystyle\int \displaystyle\frac{1}{x^2+2x}\enspace dx\)
④ \(\displaystyle\int^{4}_{1} \displaystyle\frac{1}{x^2-2x+4}\enspace dx\)

まとめ④指数・対数を含む積分|部分積分
① \(\displaystyle\int x^2 e^x\enspace dx\)
② \(\displaystyle\int x \log{x}\enspace dx\)

まとめ⑤三角関数のみの積分(置換・半角・積和・sin^nx公式)
①〜③の不定積分を求めよ.
① \(\displaystyle\int \displaystyle\sin^3 x\cos x\enspace dx\)
② \(\displaystyle\int \displaystyle\sin^2 x\enspace dx\)
③ \(\displaystyle\int \displaystyle\sin 3x\cos 2x\enspace dx\)
⑥ \(\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^4x\cos^2x \enspace dx\)
《発展問題》
\(\displaystyle\int\displaystyle\frac{5}{3\sin x+4\cos x}\enspace dx\)

まとめ⑥(三角関数)×(多項式)の積分
① 不定積分 \(\displaystyle\int x\sin x \enspace dx\) を求めよ.
② 不定積分 \(\displaystyle\int \displaystyle\frac{x}{\cos^2x} \enspace dx\) を求めよ.

【tanx/2の置換積分】三角関数・数学Ⅲ積分|考え方・例題演習

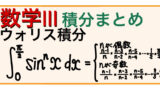
(sinx)^n、(cosx)^nの積分公式・証明・例題演習(ウォリス積分)
① \(\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^4x \enspace dx\)
② \(\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^5x \enspace dx\)
③ \(\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^4x\cos^2x \enspace dx\)







コメント