【2023数学ⅠA(第1日程)】第4問(整数の性質)
(1)問題と解答・解説《ア〜シ》

(1)解答・解説《ア〜シ》
\(462=2\times 3\times 7\times 11\)
\(110=2\times 5\times 11\) より
\(462\) と \(110\) の両方を割り切る素数のうち最大のものは \(11\) ・・・《アイ》
\(462\) と \(110\) の最小公倍数を考えればよいので
一辺の長さは,\(2\times 3\times 5\times 7\times 11=\)\(2310\) ・・・《ウ〜カ》
自然数 \(x\),\(y\) を用いて
\(|462x-110y|\) が最小となるときを考える.
(※ただし,\(|462x-110y|\not=0\))
\(|462x-110y|=22|21x-5y|\) より
\(x=1\) ,\(y=4\) のとき
差の絶対値は最小値 \(22\) ・・・《キク》
\(110y=462x+22\) のとき
\(21x-5y=-1\)
これを満たす解の \(1\) つは,\((x,y)=(4,17)\)
\(21x-5y=-1\) \(\iff\) \(y=\displaystyle\frac{21}{5}x+\displaystyle\frac{1}{5}\) より
整数 \(k\) を用いて,
\(x=5k+4\) ,\(y=21k+17\) と表せる.

この中で \(x\) が最小の自然数となるのは,\(k=0\) のとき \(x=4\)
したがって,横の長さが最小であるものは,
横の長さが \(462\times 4=\)\(1848\) ・・・《ケ〜シ》
(2)問題と解答・解説《ス〜ソ》
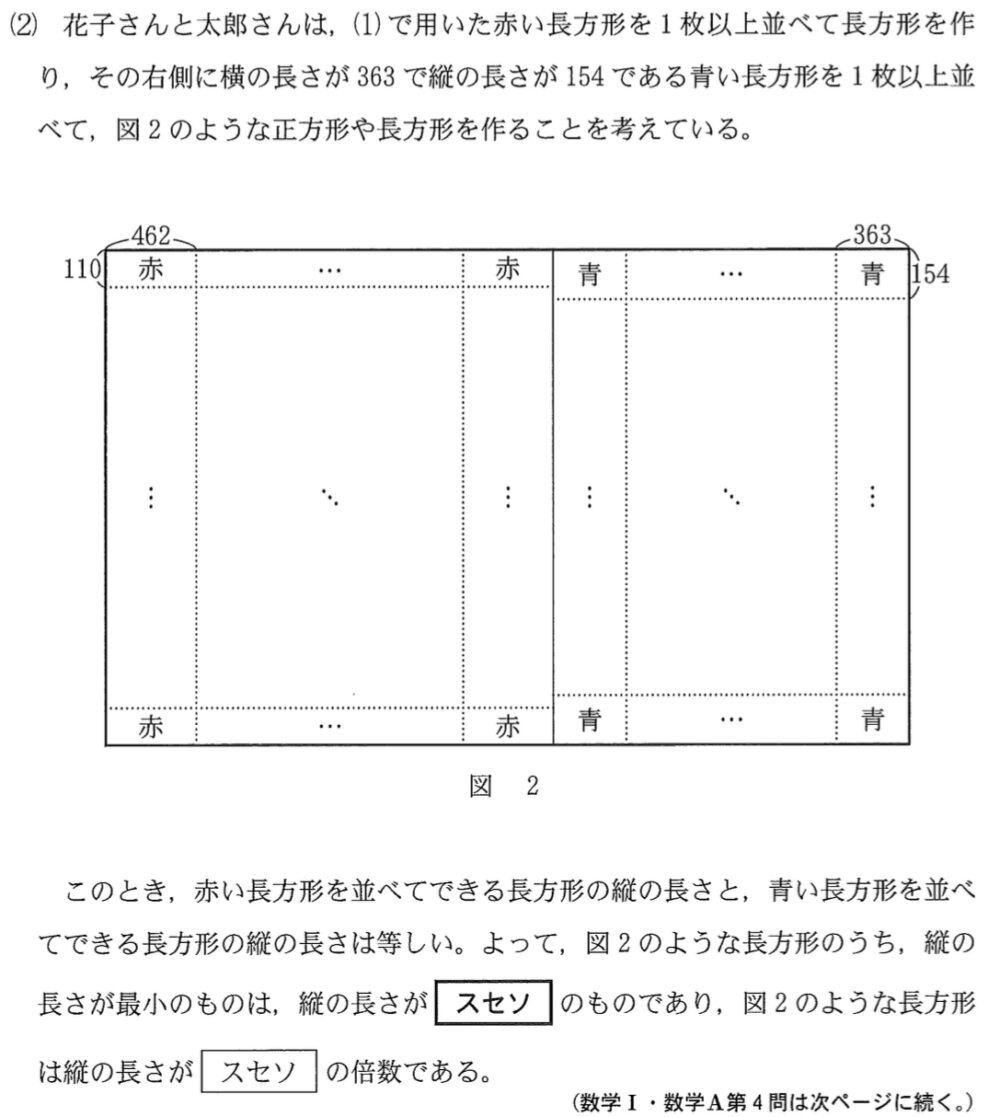
(2)解答・解説《ス〜ソ》
赤い長方形を並べてできる長方形の縦の長さと,青い長方形を並べてできる長方形の縦の長さが等しく,縦の長さが最小とするには,\(110\) と \(154\) の最小公倍数を考えればよい.
\(110=2\times 5\times 11\)
\(154=2\times 7\times 11\) より
最小公倍数は \(2\times 5\times 7\times 11=\)\(770\) ・・・《ス〜ソ》
(2)問題と解答・解説《タ〜ノ》

(2)解答・解説《タ〜ノ》
\(462=2\times 3\times 7\times 11\)
\(363=3\times 11^2\) より
最大公約数は \(3\times 11=\)\(33\) ・・・《タチ》
また
\(33=3\times 11\)
\(770=2\times 5\times 7\times 11\) より
\(33\) と \(770\) の最小公倍数は \(2\times 3\times 5\times 7\times 11=\)\(2310\) ・・・《ツ〜ナ》
ここで,赤い長方形を横に \(a\) 枚,青い長方形を横に \(b\) 枚( \(a\),\(b\) は自然数 )並べるとき
図 \(2\) の横の長さは \(462a+363b\)
これが \(2310\) の倍数 かつ 最小であるものを考える.
自然数 \(n\) を用いて
\(462a+363b=2310n\)
\(\iff\) \(14a+11b=70n\)
\(\iff\) \(11b=14(5n-a)\)
\(11\) と \(14\) は互いに素であるから,自然数 \(m\) を用いて
\(5n-a=11m\) ,\(b=14m\)
よって,\(a=5n-11m\),\(b=14m\)
\(a≧1\),\(m≧1\) なので \(a=5n-11m\) より \(n≧3\) となる.
\(n=3\) とすると,\(m=1\) ,\(a=4\) ,\(b=14\) となり条件をみたす.
以上より求める値は,\(2310\times 3=\)\(6930\) ・・・《ニ〜ノ》







コメント