【2023京都大学・文系・第3問】
(1) \(\cos 2\theta\) と \(\cos 3\theta\) を \(\cos \theta\) の式として表せ.
(2) 半径 \(1\) の円に内接する正五角形の一辺の長さが \(1.15\) より大きいか否かを理由を付けて判定せよ.
解答・解説
(1) \(2\) 倍角,\(3\) 倍角の公式の証明

記述の問題ですので,公式の結論のみでなく,証明を与えておきます。
もちろん結論のみでも○かもしれませんが,採点基準は大学にありますので,安全な解答を作成しておきましょう!
加法定理より
\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\) ・・・①
\(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\) ・・・②
②において \(\alpha=\beta=\theta\) とすると
\(\cos 2\theta=\cos^2\theta-\sin^2\theta=\cos^2\theta-(1-\cos^2\theta)\)
よって,\(\cos 2\theta=2\cos^2\theta-1\)
次に,②において \(\alpha=2\theta\),\(\beta=\theta\) とすると
\(\cos3\theta=\cos 2\theta\cos\theta-\sin 2\theta\sin\theta\)
ここで①において \(\alpha=\beta=\theta\) とすると
\(\sin 2\theta=2\sin \theta\cos \theta\) より,これと \(\cos 2\theta=2\cos^2\theta-1\) から
\(\cos3\theta=(2\cos^2\theta-1)\cos\theta-2\sin ^2\theta\cos\theta\)
\(=(2\cos^2\theta-1)\cos\theta-2(1-\cos^2 \theta)\cos\theta\)
よって,\(\cos 3 \theta=4\cos^3 \theta-3\cos \theta\)
(2) 半径 \(1\) の円に内接する正五角形の一辺の長さ

正五角形を扱う上で、\(36°\) や \(72°\) の三角比が必要になります。
頻出の有名な値になりますので,結果を覚えるだけでなく,導き方も押さえておきましょう!

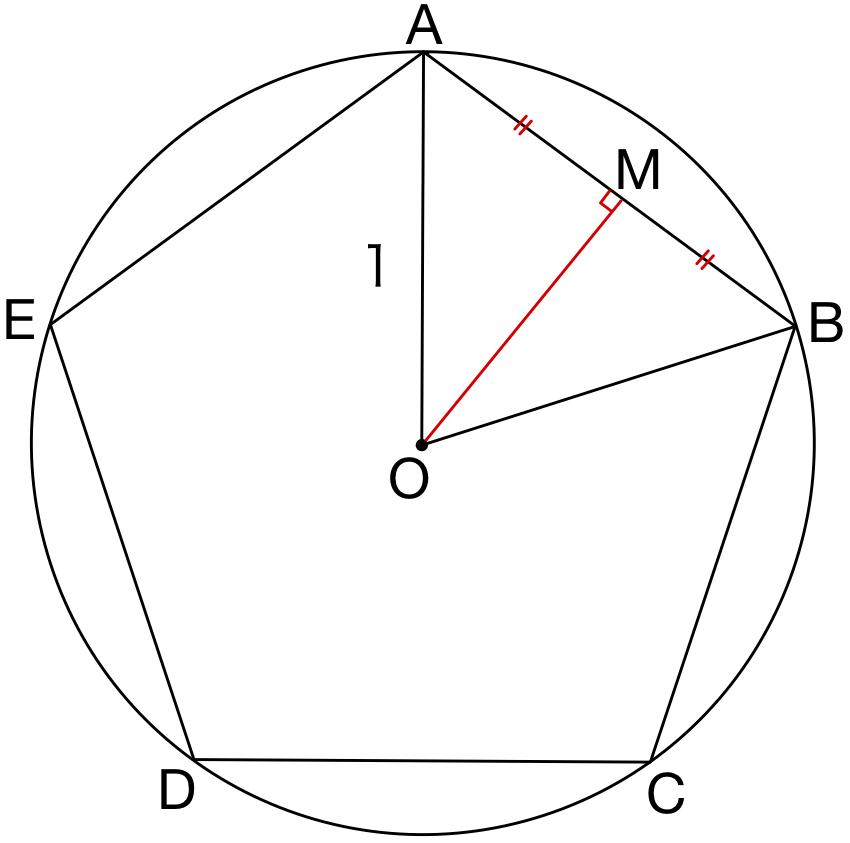 右図のように,正五角形 \(ABCDE\) の外接円の中心を \(O\),辺 \(AB\) の中点を \(M\) とおく.
右図のように,正五角形 \(ABCDE\) の外接円の中心を \(O\),辺 \(AB\) の中点を \(M\) とおく.
このとき,\(OA=OB=1\),\(\angle AMO=90°\),\(\angle AOM=36°\) となる.
直角三角形 \(OAM\) に注目すると
\(\sin\angle AOM=\displaystyle\frac{AM}{OA}\)
\(\iff\) \(AM=OA\sin\angle AOM=\sin 36°\)
\(AB=2AM=2\sin 36°\) となる.
ここで,\(\theta=36\text{°}\) とおく.
\(5\theta=180\text{°}\) より
\(3\theta=180\text{°}-2\theta\)
\(\cos 3\theta=\cos (180\text{°}-2\theta)=-\cos 2\theta\)
(1)の結果から
\(4\cos^3\theta-3cos \theta=-(2\cos^2\theta-1)\)
\(4\cos^3\theta+2\cos^2\theta-3cos \theta-1=0\)
\(x=\cos \theta\) とおくと,\(\theta=36\text{°}\) より \(0<x<1\)
\(4x^3+2x^2-3x-1=0\)
左辺を \(f(x)\) とおくと
\(f(-1)=0\) なので
\((x+1)(4x^2-2x-1)=0\)
\(x=-1\),\(\displaystyle\frac{1\pm\sqrt{5}}{4}\)
\(0<x<1\) より
\(x=\displaystyle\frac{1+\sqrt{5}}{4}\)
よって,\(\cos \theta=\displaystyle\frac{1+\sqrt{5}}{4}\)
したがって,\(AB=2\sin \theta=\sqrt{\displaystyle\frac{5-\sqrt{5}}{2}}\)
\(AB^2-1.15^2=\displaystyle\frac{5-\sqrt{5}}{2}-\left(\displaystyle\frac{23}{20}\right)^2=\displaystyle\frac{471-200\sqrt{5}}{400}\)
\(2.2^2<\sqrt{5}^2<2.3^2\) より \(2.2<\sqrt{5}<2.3\) なので
\(200\sqrt{3}<460\) であるから,\(471-200\sqrt{5}>0\)
ゆえに,\(AB^2-1.15^2>0\) より \(AB>1.15\)
したがって,正五角形の一辺の長さは \(1.15\) より大きい.








コメント