 場合の数・確率
場合の数・確率 【2006京都大学・後期・第3問】n個のさいころの和がn+3になる確率
実験から答え・方針を予想する練習にもってこいの良問。答えを見て分かった気になっている勉強では確率は力がつかない。正しい確率の勉強の仕方を学び、考え方・方針の立て方をこの1問から学びましょう。2次試験対策、数学A確率。
 場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率 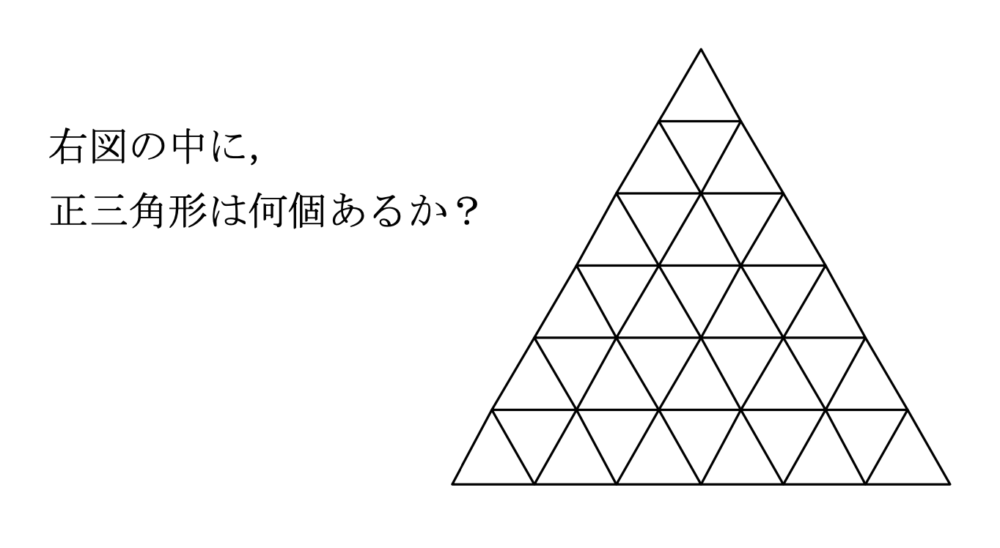 場合の数・確率
場合の数・確率