不等式の証明（凸関数の利用）

はじめに

ここでは発展的な考え方を使って、不等式の証明を考えます。

基本的な不等式の証明については

【数学Ⅱ】不等式の証明（まとめ）解法５つ

にまとめてありますので、そちらをご確認ください。

今回の問題については、おそらく学校の授業では扱いわないと思います。

今まで一度も経験したことのない発想だと思いますので、例題を使って考え方・解答を紹介しますので、それを読んだ後に再度チャレンジしてみてください！

【例題】相加平均・相乗平均の関係の証明

【証明】凸関数を利用した証明

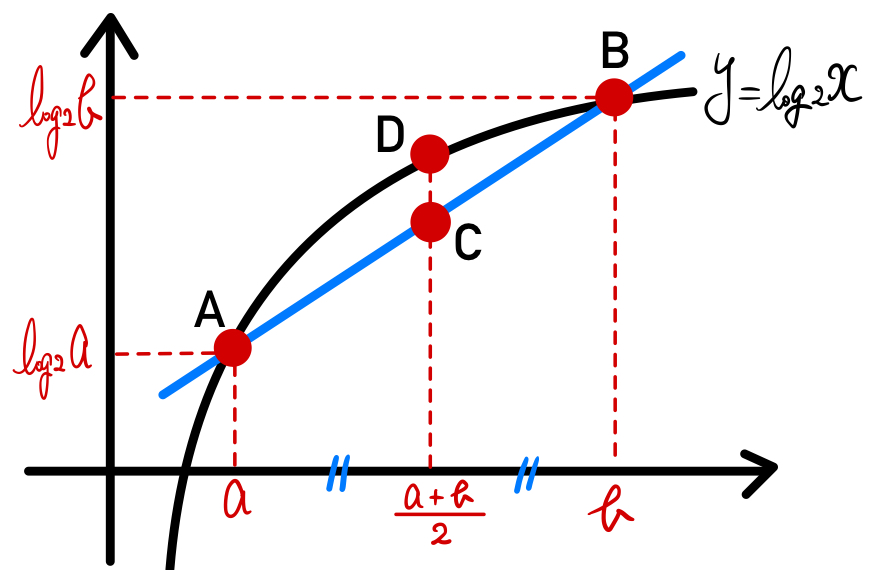
上図のように $y=log_{2}x$ のグラフ上に 2 点

$A ( a , log_{2}a )$、$B ( b , log_{2}b )$ を考える．

ただし、$0<a≦b$ とする．

このとき、2 点A、B の中点を C とすると、

C $( \displaystyle\frac{a+b}{2} , \displaystyle\frac{log_{2}a+ log_{2}b}{2})$

また、$x=\displaystyle\frac{a+b}{2}$ と $y=log_{2}x$ の交点を D とする．

つまり D $( \displaystyle\frac{a+b}{2} , log_{2}\displaystyle\frac{a+b}{2} )$ ．

このとき、$y=log_{2}x$ のグラフは上に凸の関数であるから、

(点 C の $y$ 座標) ≦ (点 D の $y$ 座標)

よって、

$\displaystyle\frac{log_{2}a+ log_{2}b}{2}≦log_{2}\displaystyle\frac{a+b}{2}$

$\displaystyle\frac{1}{2}log_{2}ab≦log_{2}\displaystyle\frac{a+b}{2}$

$log_{2}(ab)^{\displaystyle\frac{1}{2}}≦log_{2}\displaystyle\frac{a+b}{2}$

$y=log_{2}x$ は増加関数であるから、

$\sqrt{ab}≦\displaystyle\frac{a+b}{2}$

したがって、

$a+b≧2\sqrt{ab}$

等号成立は

( 点 C の $y$ 座標 ) と ( 点 D の $y$ 座標 ) が一致するとき、

つまり、点 A と点 B が一致するときであるから、$a=b$ のときである．

補足

※本問では底を 2 とする対数で考えたが、3 でも 4 でも何でも良い．

※$y=log_{2}x$ のグラフは上に凸の関数であることは、

数学Ⅲの履修者は $y^{\prime\prime}$ の符号を考える必要がある．

【問題】解答

$0≦x<\displaystyle\frac{\pi}{2}$ で $y=\tan x$ のグラフは下に凸のグラフである．

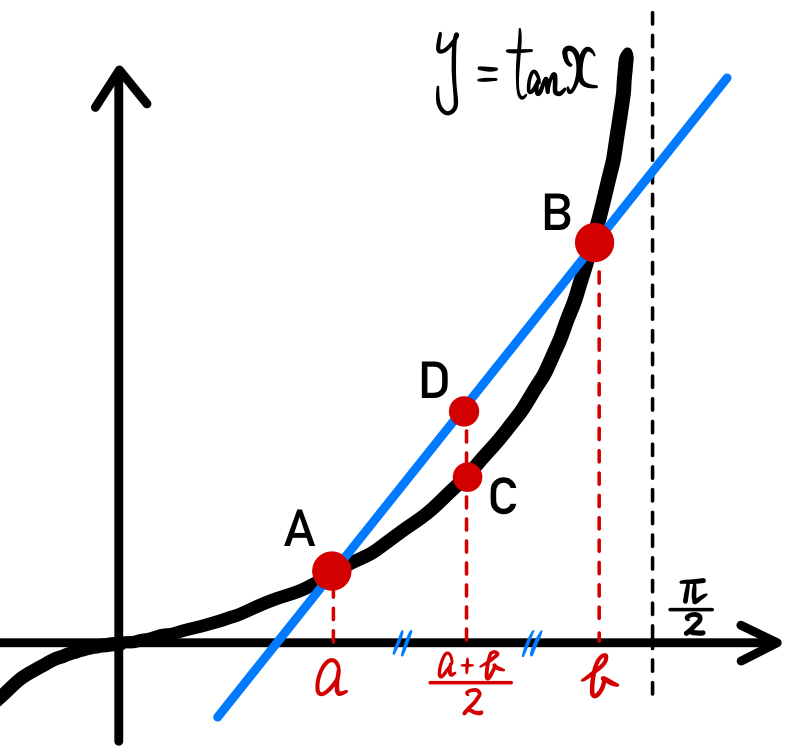
(ⅰ)　$a<b$ のとき

A $( a , \tan a )$、B $( b , \tan b )$ とおき、図のように 2 点 C 、 D をとると、

C $(\displaystyle\frac{a+b}{2} , \displaystyle\frac{\tan a+\tan b}{2})$

D $(\displaystyle\frac{a+b}{2} , \tan \displaystyle\frac{a+b}{2})$

C と D の $y$ 座標に注目すると、

$\tan \displaystyle\frac{a+b}{2}<\displaystyle\frac{1}{2}(\tan a+\tan b)$ が成立．

(ⅱ)　$a=b$ のとき

(左辺)$=\tan \displaystyle\frac{a+a}{2}=\tan a$

(右辺)$=\displaystyle\frac{1}{2}(\tan a+\tan a)= \tan a$

したがって、$a=b$ のとき等号が成立する．

(ⅲ) 　$a>b$ のとき

(ⅰ)と同様に考えて成立する．

したがって、題意は示された．

最後に

今回のテーマは難易度の高いテーマでした。

経験なしにこのような発想はさすがにできないと思います。

ただ網羅系で有名な問題集である「標準問題精講　数学 Ⅱ 」などにも記載されている考え方になります。

※標準問題精講にはもっと難しい形で出題されています。