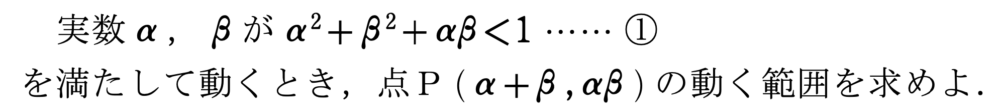
簡単ですか？？
この問題は本当に差がつく問題で、頻出問題の１つ。
そして、多くの受験生が満点が取れない問題でも有名です。
よくある間違い解答（不十分な解答）
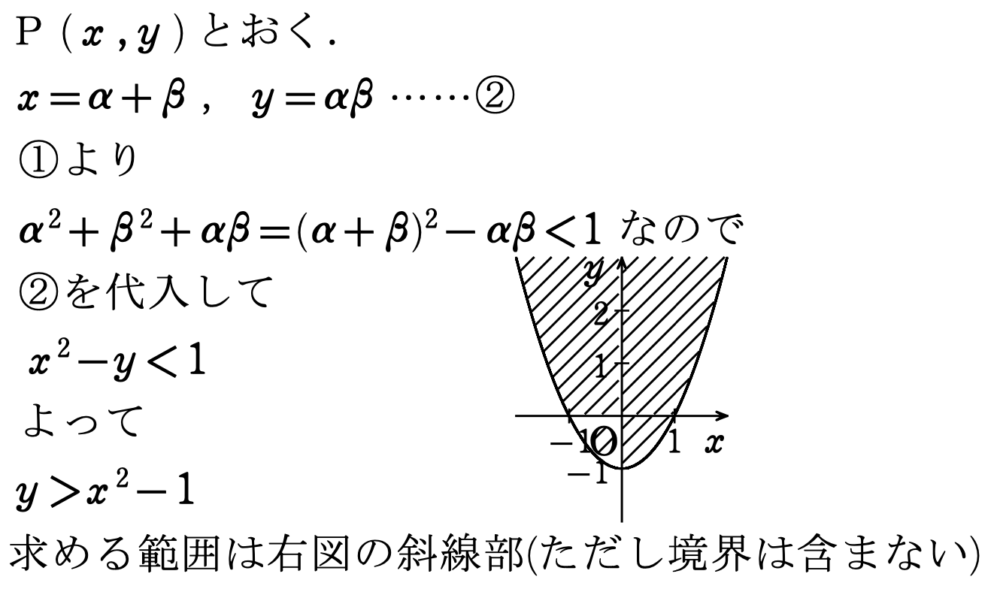
上の解答は不正解です。どこが間違えているか分かりますか？
考え方
α，βが実数解をもつ条件
👉解と係数の関係 & 判別式が 0 以上
模範解答
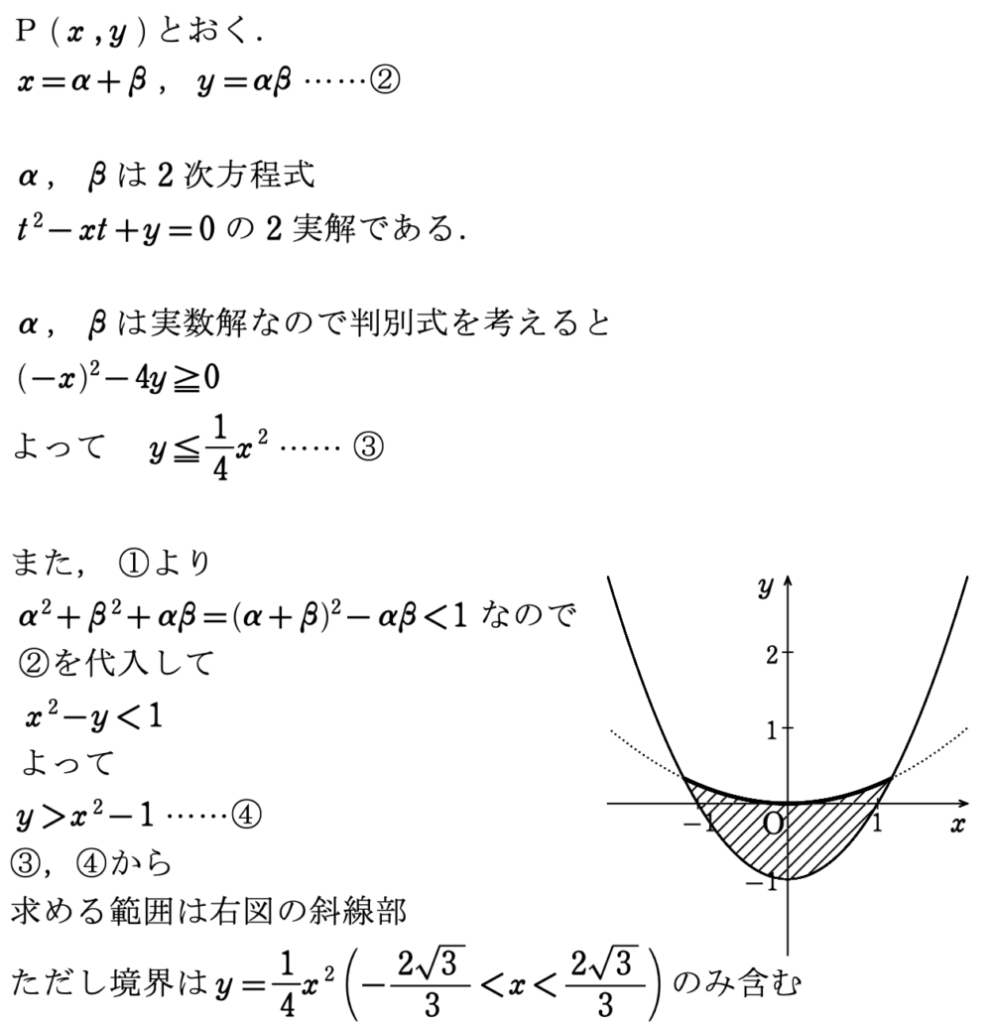
いかがだったでしょうか？
初見では引っかかってしまう問題。
しかし頻出テーマになりますので、必ず一度経験値を積み、他の受験生と差がつけられるように演習をしておきましょう。
2018京都大学｜n^3-7n+9が素数となるn(文系第３問、理系第２問)
素数に関する有名頻出問題。数学の２次試験で差がつきやすい整数分野の問題について、ただ答えが出せるだけの勉強ではなく、どのように考えるのか、思考過程を丁寧に解説。同じ問題は出ませんが、同じ形式の問題は出題されます。しっかりと考え方を学び、２次数学でしっかり得点源に！
mathmathmanabu.com
2021.07.19
【差がつく考え方】平面図形の３つのアプローチ！(幾何・座標・ベクトル)
２次試験の数学において、平面図形は合否を分けることがよくあります。幾何、座標、ベクトルの３タイプのアプローチの仕方を学びましょう。最後まで解けなくても、部分点を取ることが大切。練習でできないことは本番ではできません！
mathmathmanabu.com
2021.07.04
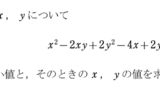
2変数関数の最大値・最小値【１文字固定法（予選決勝法）】
１文字固定（予選決勝法）と言われる大学受験では頻出テーマについて考え方を身につけよう。
２次関数の最大値、最小値。数学２次試験対策。頻出・良問
mathmathmanabu.com
2021.07.04
コメント