【大阪大学】
条件 \(1<x<2^{n+1}\) および \(0<y≦\log_{2}{x}\) を満たす整数 \(x\) , \(y\) を座標とする点 \((x,y)\) の個数を求めよ．
格子点問題の考え方
格子点
⇒ \(x\) or \(y\) 軸に平行な直線ごとにカウントし，総和(Σ)を考える
【格子点】x+y≦n(x,yは0以上の整数)を満たす格子点の個数｜2014中央大学
x,y座標がともに整数となる格子点の個数の数え方・考え方を解説。x＝kやy＝k上の格子点を数え、総和(シグマ)を考える。難関大学頻出・有名問題。差がつく入試問題。数学A：整数問題、数学B：数列。2014中央大学過去問演習。GMARCH、関関同立、早慶、東大、京大、一橋、旧帝大、難関大学対策。
mathmathmanabu.com
2022.07.28
【格子点】放物線と直線で囲まれた領域の格子点の個数｜お茶の水女子大学
x,y座標がともに整数となる格子点の個数の数え方・考え方を解説。x＝kやy＝k上の格子点を数え、総和(シグマ)を考える。難関大学頻出・有名問題。差がつく入試問題。数学A：整数問題、数学B：数列。お茶の水女子大学過去問演習。GMARCH、関関同立、早慶、東大、京大、一橋、旧帝大、難関大学対策。
mathmathmanabu.com
2022.07.29
解答・解説
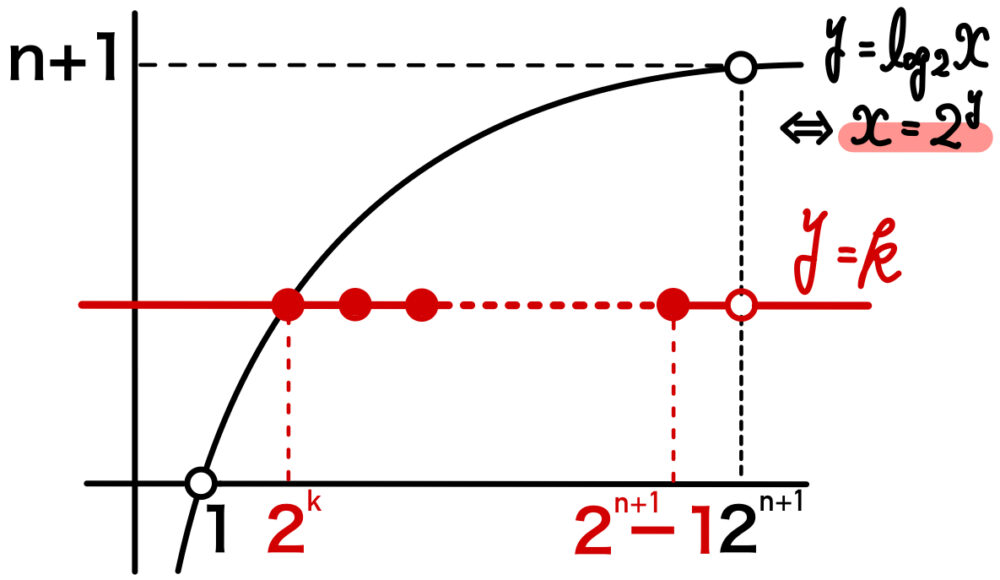
条件 \(1<x<2^{n+1}\) および \(0<y≦\log_{2}{x}\) を満たす領域において
\(y=k\) ( \(1≦k≦n\) ) 上には
\((2^k,k)\) , \((2^k+1,k)\) , \((2^k+2,k)\) , \(\cdots\) , \((2^{n+1}-1,k)\) の
\((2^{n+1}-1)-2^k+1=2^{n+1}-2^k\) 個の格子点がある．
よって，
\(\displaystyle\sum_{k=1}^{n}{(2^{n+1}-2^k)}\)
\(=n\cdot2^{n+1}-\displaystyle\frac{2(2^n-1)}{2-1}\)
\(=(n-1)2^{n+1}+2\)
コメント