〔2〕問題《シ》
〔2〕解答・解説《シ》
以下において,\(\angle DCP=\theta\) とおく.
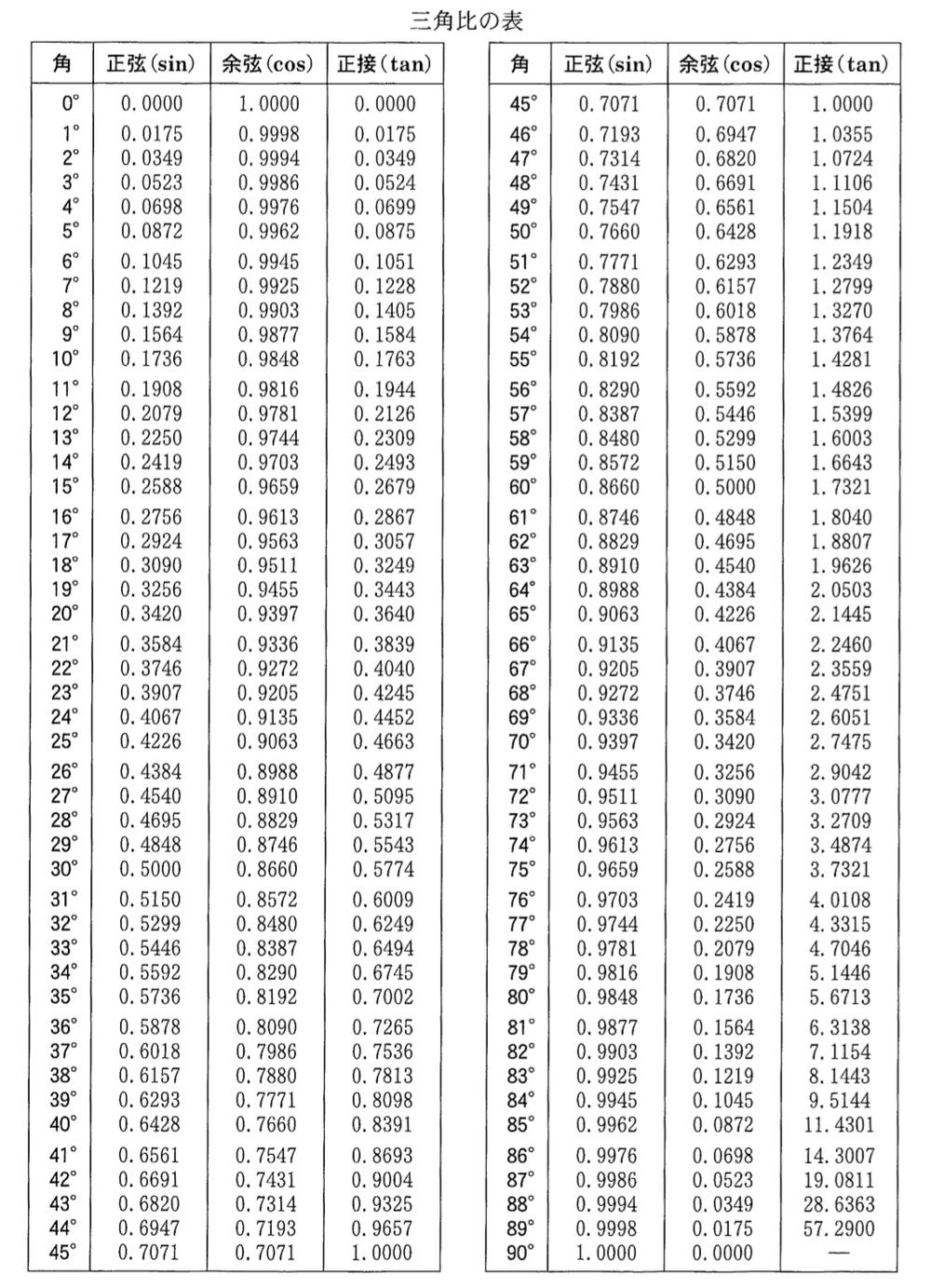
\(\tan\theta=\displaystyle\frac{7}{100}=0.07\) で三角比の表(※三角比の表はページ下部)から
\(4°<\theta<5°\)
よって \(n=4\) ・・・《シ》
〔2〕問題《ス~ツ》
〔2〕解答・解説《ス~ツ》
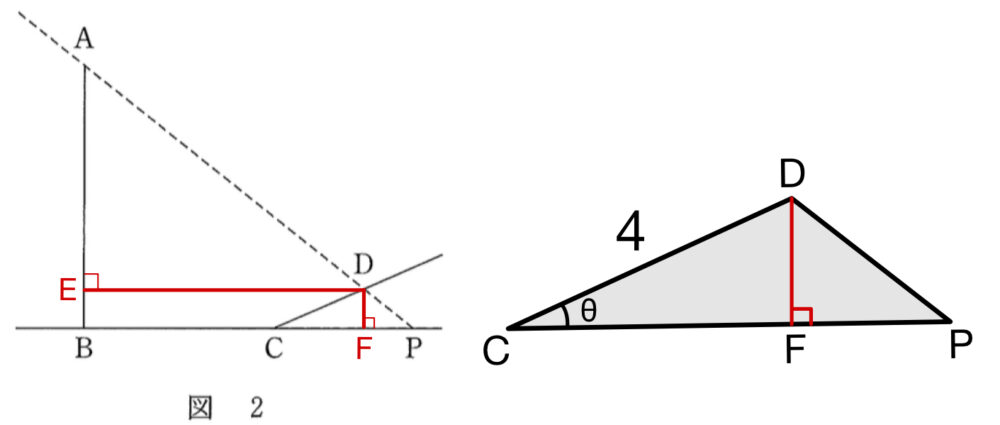
図のように,点DからAB,BCに下した垂線の足をE,Fとする.
三角形CDFに注目すると
\(\sin\theta=\displaystyle\frac{DF}{CD}=\displaystyle\frac{BE}{4}\)
\(BE=4\times \sin\theta\) ・・・《スセ》であり
また \(\cos\theta=\displaystyle\frac{CF}{CD}=\displaystyle\frac{CF}{4}\)
よって \(CF=4\times\cos\theta\)
\(ED=BF=BC+CF=7+4\times\cos\theta \) ・・・《ソ~チ》
\(\angle APB=45°\) のとき,三角形ADEはAE=DEの直角二等辺三角形であるから,
電柱の高さは,
\(AB=AE+BE=(7+4\times\cos\theta)+ 4\times \sin\theta \)
三角比の表から,\(\sin\theta=\sin 4°=0.0698\),\(\cos\theta=\cos 4°=0.9976\) より
\(AB=11.2696≒\)\(11.3\) ・・・《ツ》
〔2〕問題《テ~ニ》
〔2〕解答・解説《テ~ニ》
\(BE=DF=CD\times\sin\theta\),\(CF=CD\times \cos\theta\) より
\(ED=BC+CF=7+ CD\times \cos\theta \)
ここで,三角形ADEで \(\angle ADE=42°\) より
\(\tan 42°=\displaystyle\frac{AE}{ED}\) \(\iff\) \(AE=ED\times\tan 42°=(7+ CD\times \cos\theta) \times\tan 42°\)
\(AB=AE+BE=(7+ CD\times \cos\theta) \times\tan 42°+ CD\times\sin\theta \)
\(CD(\cos\theta\times\tan 42°+\sin\theta)=AB-7 \times\tan 42°\)
したがって,\(CD=\displaystyle\frac{ AB-7 \times\tan 42°}{\cos\theta\times\tan 42°+\sin\theta }\) ・・・《テ~二》
ここに必要な値を三角比の表から読み取り代入すると,CDの長さ(影の長さ)がわかる.

三角比の表







コメント