【4STEP 162(2)】
次の関数に最大値、最小値があれば、それを求めよ.
\(y=(x^2-2x)^2+4(x^2-2x)-1\)
置き換え⇒範囲チェック!
数学を勉強する上で、最重要ポイントの1つになります!
そこで、\(t=x^2-2x\) と置き換えをし、\(2\) 次関数に変形しましょう!
その際に重要になるのが、置き換えた文字の範囲を確認することです!
補足:どうして範囲の確認が必要なのか
本問では \(x\) に範囲がないにもかかわらず、なぜ置き換えをした \(t\) の範囲を確認する必要があるのか??
具体的な例を用いて、範囲を確認する必要性を確認しておきましょう!
・\(t=x^2-2x\) と置いたとき
例① \(t=3\) のとき
\(x^2-2x=3\) \(\iff\) \(x^2-2x-3=0\) \(\iff\) \((x+1)(x-3)=0\)
したがって、\(x=-1,3\)
👉 \(x=-1,3\) とすれば、\(t=3\) という値を取りうることができるということ!
例② \(t=-3\) のとき
\(x^2-2x=-3\) \(\iff\) \(x^2-2x+3=0\)
解の公式を考えると、
\(x=1\pm\sqrt{-2}=1\pm\sqrt{2}i\)
👉 \(t=-3\) を取りうる実数 \(x\) は存在しない!
つまり、\(t=-3\) を考えることはダメだということ!
このように存在しない \(t\) が存在するため、置き換えた文字 \(t\) について、範囲の確認が必要となります!
範囲の確認はグラフをかく!
それではどのように置き換えた文字の範囲を確認すれば良いのか?
様々な確認の仕方はありますが、1番確実なものは、グラフを描く(視覚的に考える)ことです。
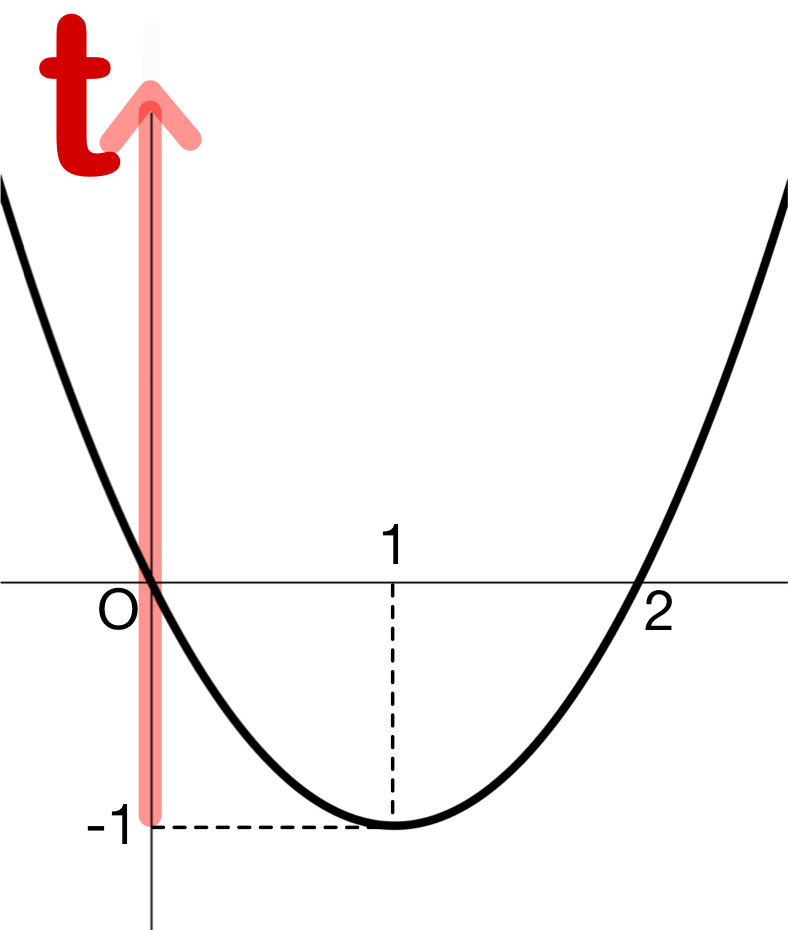
本問では、\(t=x^2-2x\) と置き換えをしたので、
\(t=(x-1)^2-1\) であるから、
グラフをかくと左図のようになり、
\(t\) が存在するのは \(-1\) 以上であることがわかります。
したがって、\(t≧-1\) になります。
解答
\(y=(x^2-2x)^2+4(x^2-2x)-1\) ・・・①
①において、\(t=x^2-2x\) とおくと
\(y=t^2+4t-1=(t+2)^2-5\) ・・・②
また、\(t=x^2-2x\) より
\(t=(x-1)^2-1\) であるから、\(t≧-1\) ・・・③
②、③より、グラフを考えると、
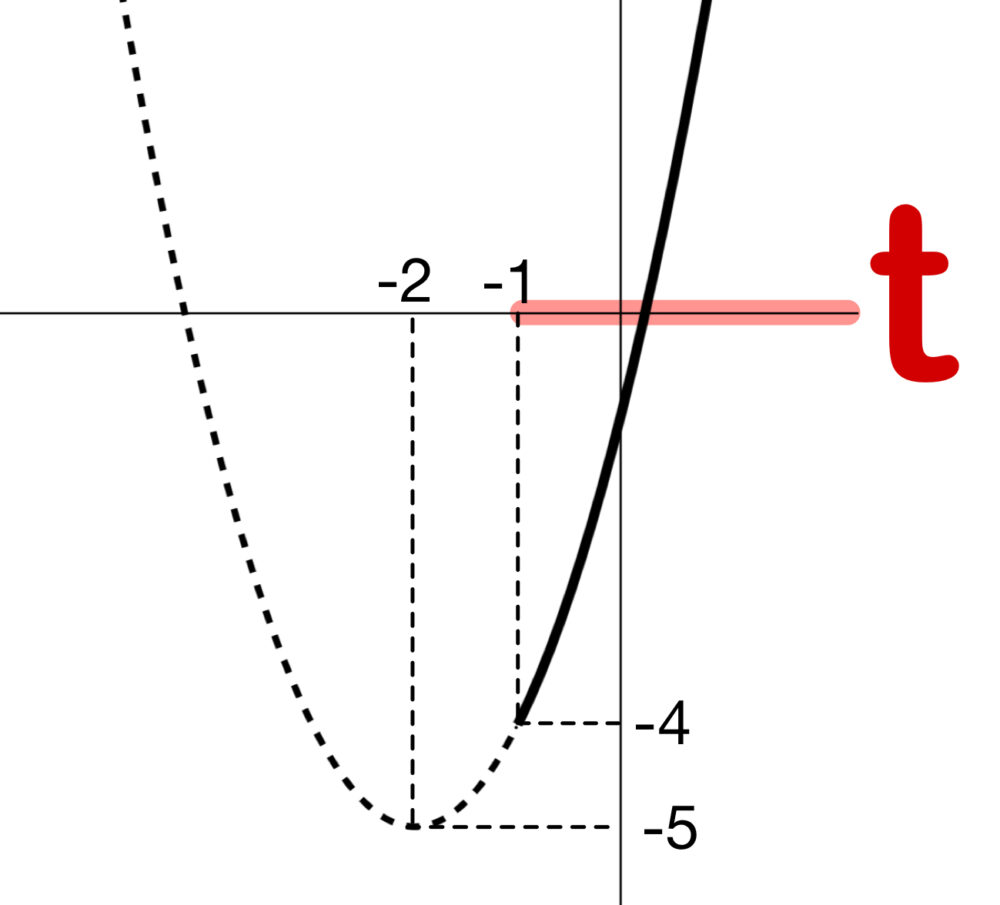
\(y\) は \(t=-1\) で最小値 \(-4\) をとる.
このとき、\(x^2-2x=-1\) \(\iff\) \((x-1)^2=0\) \(\iff\) \(x=1\)
ゆえに、\(x=1\) のとき最小値 \(-4\)
最大値はない。
最後に
本問では、2次式を別の文字で置き換えた上で、2次関数に落とし込みました。
三角比や指数・対数を \(t\) と置き換え、範囲を考えた上で、2次関数に落とし込み最大・最小を考えるなど、他分野でも同じように考える問題は多数あります。
「置き換えをしたら範囲の確認」という超重要ポイントを、1つの合言葉としてマスターし、様々な問題で応用できるようにしていきましょう!








コメント