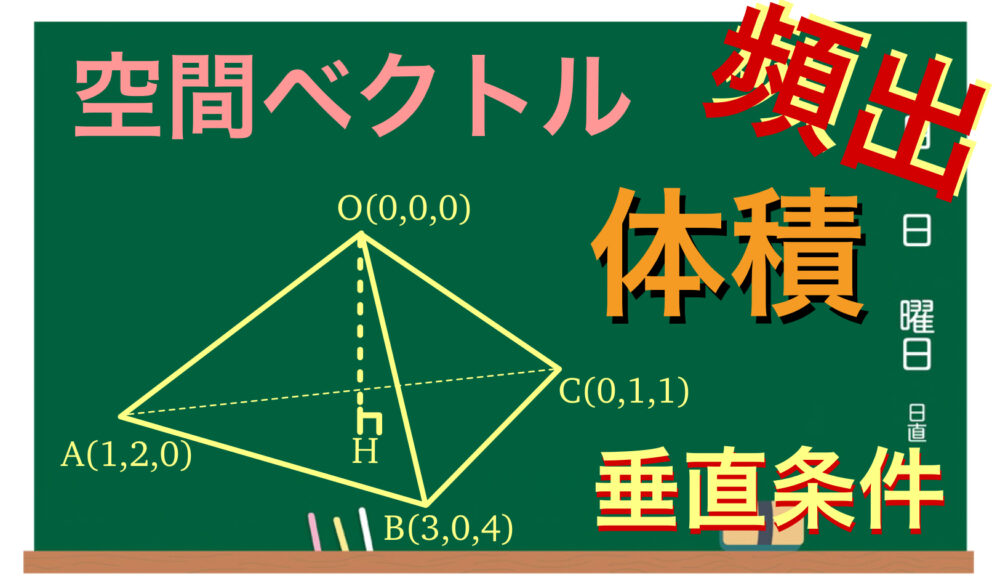
\(4\) 点 \(O ( 0 , 0 , 0 )\) , \(A ( 1 , 2 , 0 )\) , \(B ( 3 , 0 , 4 )\) , \(C ( 0 , 1 , 1 )\) がある．
四面体 \(OABC\) の体積を求めよ．
【重要公式】三角形の面積公式(ベクトル)
体積の高さについて
点 \(O\) から平面 \(ABC\) に下ろした垂線の足を \(H\) とおく．このとき
点 \(H\) は
① 平面 \(ABC\) 上 ⇒ 共面条件の利用
② \(OH\perp 平面ABC\) ⇒ 垂直条件
共面条件
共面条件とは，異なる \(4\) 点が同一平面上に並ぶときの条件
（※ \(4\) 点が同一直線状であるときは除く）
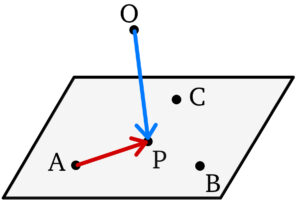\(4\) 点 \(A\)，\(B\)，\(C\)， \(P\) が同一平面上にあるとき
① \(A\) を始点として考える( \(k\)，\(l\) は実数 )
\(\overrightarrow{AP}=k\overrightarrow{AB}+l\overrightarrow{AC}\)
② \(O\) を始点として考える( \(s\)，\(t\)，\(u\) は実数 )
\(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}+u\overrightarrow{OC}\) かつ \(s+t+u=1\)
垂直条件
平面 \(\alpha\) 上の異なる \(2\) つのベクトル \(\overrightarrow{x}\) , \(\overrightarrow{y}\) ( ただし，\(\overrightarrow{x}\) , \(\overrightarrow{y}\) は零ベクトルでなく，互いに平行ではない ) に対して，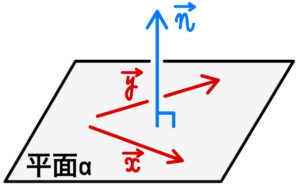
平面 \(\alpha\) \(\perp \overrightarrow{n}\)
\(\iff\) \(\overrightarrow{x} \perp \overrightarrow{n}\) かつ \(\overrightarrow{y} \perp \overrightarrow{n}\)
\(\iff\) \(\overrightarrow{x}\cdot\overrightarrow{n}=0\) かつ \(\overrightarrow{y}\cdot\overrightarrow{n}=0\)
解答
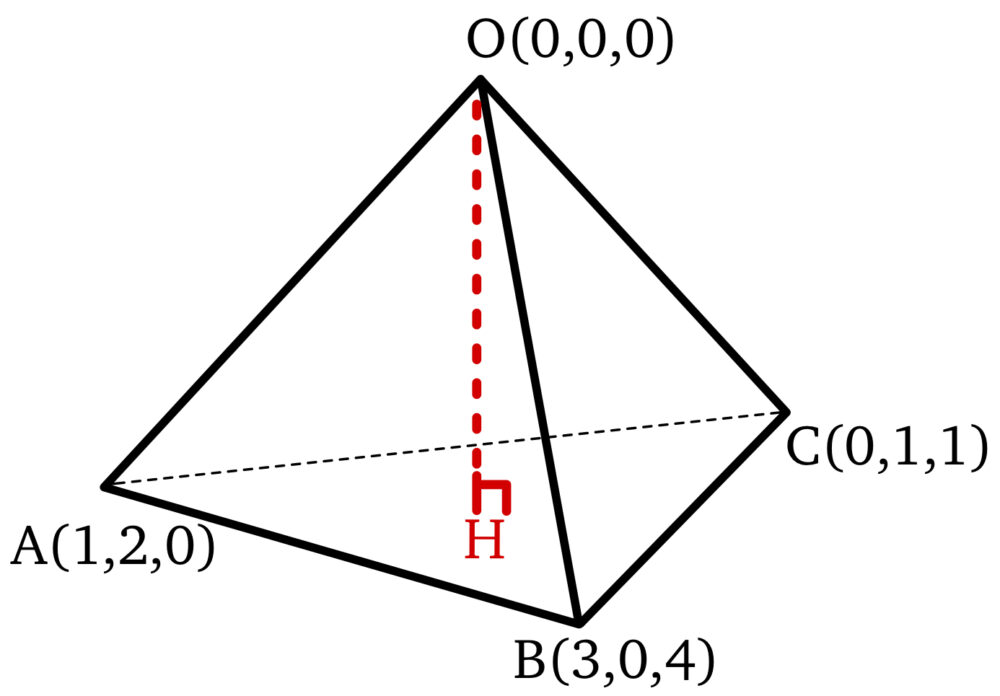
(※ 上図はイメージです．正確な位置関係ではありません)
\(\overrightarrow{AB}=( 2 , -2 , 4 )\) , \(\overrightarrow{AC}=( -1 , -1 , 1 )\) より
\(|\overrightarrow{AB}|=\sqrt{2^2+(-2)^2+4^2}=2\sqrt{6}\) ,
\(|\overrightarrow{AC}|=\sqrt{(-1)^2+(-1)^2+1^2}=\sqrt{3}\) ,
\(\overrightarrow{AB}\cdot\overrightarrow{AC}=2\times (-1)+(-2)\times (-1)+4\times 1=4\) より
\(\triangle ABC=\displaystyle\frac{1}{2}\sqrt{(2\sqrt{6})^2(\sqrt{3})^2-4^2}=\sqrt{14}\)
次に，点 \(O\) から平面 \(ABC\) に下ろした垂線の足を \(H\) とおく．
このとき，点 \(H\) は平面 \(ABC\) 上より実数 \(s\) , \(t\) を用いて
\(\overrightarrow{AH}=s\overrightarrow{AB}+t\overrightarrow{AC}\) とおける．
よって，\(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{AH}=\overrightarrow{OA}+s\overrightarrow{AB}+t\overrightarrow{AC}\) であるから，
\(\overrightarrow{OH}=( 1 , 2 , 0 )+s( 2 , -2 , 4 )+t( -1 , -1 , 1 )\)
\(=( 2s-t+1 , -2s-t+2 , 4s+t )\) ・・・①
また，\(OH\perp 平面ABC\) より，
\(\overrightarrow{OH}\perp\overrightarrow{AB}\) かつ \(\overrightarrow{OH}\perp\overrightarrow{AC}\)
・\(\overrightarrow{OH}\perp\overrightarrow{AB}\) のとき
\(\overrightarrow{OH}\cdot\overrightarrow{AB}=0\)
\(2(2s-t+1)-2(-2s-t+2)+4(4s+t)=0\)
よって、\(12s+2t-1=0\) ・・・②
・\(\overrightarrow{OH}\perp\overrightarrow{AC}\) のとき
\(\overrightarrow{OH}\cdot\overrightarrow{AC}=0\)
\(-(2s-t+1)-(-2s-t+2)+(4s+t)=0\)
よって、\(4s+3t-3=0\) ・・・③
②，③より \(s=\displaystyle\frac{-3}{28}\) , \(t=\displaystyle\frac{8}{7}\)
①より，
\(\overrightarrow{OH}=\left(\displaystyle\frac{-5}{14},\displaystyle\frac{15}{14},\displaystyle\frac{5}{7}\right)=\displaystyle\frac{5}{14}(-1,3,2)\)
よって，\(|\overrightarrow{OH}|=\displaystyle\frac{5}{14}\sqrt{(-1)^2+3^2+2^2}=\displaystyle\frac{5\sqrt{14}}{14}\)
したがって求める体積は，
\(\displaystyle\frac{1}{3}\times \sqrt{14}\times \displaystyle\frac{5\sqrt{14}}{14}=\displaystyle\frac{5}{3}\)
別解：平面の方程式・点と面の距離の公式
ほとんどの学校で学習しないかもしれませんが，数学Bのベクトルの発展として記載されている範囲です。
もちろん知らなくても解けますが，知っていると計算が楽になったり，より複雑な問題を簡単に処理することができます！
ちなみに，京都大学では頻出のテーマの１つです！
差がつく範囲として余力がある方は勉強してみましょう！
公式・例題等については，「京都大学頻出（空間ベクトル）平面の方程式・点と平面の距離の公式」にまとめています。ご参考に。
コメント