
【問題①】
直線 \(l\) を \(y=2ax-a^2\) とする.
\(a\) がすべての実数値をとって変化するとき、直線 \(l\) が通過する領域を図示せよ.
【問題②】
\(t\) が、 \(t≧0\) の実数を満たすとき、
直線 \(y=tx-t^2 +1=0\) が通過する領域を図示せよ.
※下に練習問題として「2010大阪大学」、「2015横浜国立大学」の問題あり
はじめに
数学Ⅱ(図形と方程式)の分野で超有名かつ重要・頻出問題の1つである通過領域問題について、「考え方」を中心にお話ししていきます。模範解答を見て、ただ解法を覚えるだけでは、少し問題をひねられると対応できなくなります。しっかりとした考え方を学び、応用できるように!
【問題①】
直線 \(l\) を \(y=2ax-a^2\) とする.
\(a\) がすべての実数値をとって変化するとき、直線 \(l\) が通過する領域を図示せよ.
考え方・思考の仕方
具体的な値で実験してみよう!
例①
直線 \(l\) は 点\(( 2 , -5 )\) を通るのか?
直線 \(l\) に 点\(( 2 , -5 )\) を試に代入してみると、
\(-5=4a-a^2\)
\(a^2-4a-5=0\)
\((a-1)(a+5)=0\)
\(a=-1 , 5\)
例②
直線 \(l\) は 点\(( 3 , 10 )\) を通るのか?
直線 \(l\) に 点\(( 3 , 10 )\) を試に代入してみると、
\(10=6a-a^2\)
\(a^2-6a+10=0\)
\(a=3±i\) となり、実数解をもたない
一般化して考える
直線 \(l\) は 点\(( x , y )\) を通るのか?
直線 \(l\) に 点\(( x , y )\) を試に代入してみると、
\(y=2ax-a^2\)
\(a^2-2xa+y=0\)・・・①
○ 少なくとも1つ実数解 \(a\) が存在
→ 通過する
○ 実数解 \(a\) が存在しない
→ 通過しない
①は \(a\) の2次関数と見ることができ、①が実数解を持てばよいので、
(①の判別式) \(≧0\) となればよい
【問題①の解答】
\(y=2ax-a^2\) より
\(a^2-2xa+y=0\)・・・①
①を満たす実数解 \(a\) が少なくとも1つ存在すればよいので、
(①の判別式) \(≧0\) を満たせばよい.
よって
(①の判別式) \(=(-2x)^2-4y ≧ 0\)
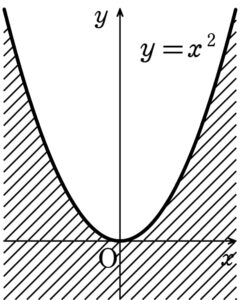
したがって \(y≦x^2\)
求める領域は、右図の斜線部で、境界線を含む.
【問題②】
\(t\) が、 \(t≧0\) の実数を満たすとき、
直線 \(y=tx-t^2 +1=0\) が通過する領域を図示せよ.
考え方・思考の仕方
基本的な考え方は、問題①と同様.
問題①との違いは、「\(t≧0\)」という範囲があるかどうか.
\(t≧0\) において、
\(t^2-xt+y-1=0\) が
少なくとも1つ実数解を持てばよい.
【問題②の解答】
\(f(t)= t^2-xt+y-1\) とおく.
軸は \(t=\displaystyle\frac{x}{2}\) より
(ⅰ) \(軸 ≦ 0\) のとき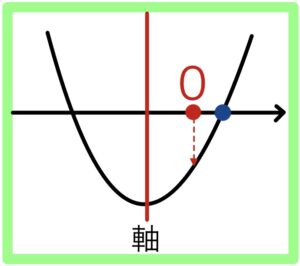
\( \displaystyle\frac{x}{2}≦0\)
つまり \(x≦0\) のとき
\(f(0)≦0\) を満たせばよい
よって \(f(0)=y-1≦0\)
\(y≦1\)
(ⅱ) \(軸 ≧ 0\) のとき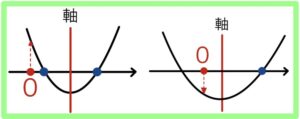
\( \displaystyle\frac{x}{2}≧0\)
つまり \(x≧0\) のとき
\(f(0)=0\) の判別式をDとすると
\(D≧0\) を満たせばよい
よって \(D=x^2-4(y-1)≧0\)
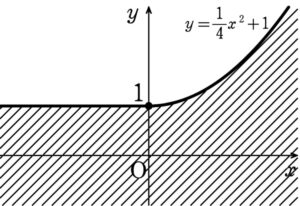
\(y≦\displaystyle\frac{x^2}{4}+1\)
(ⅰ)、(ⅱ)より求める領域は、右図の斜線部で、境界線を含む.
これまでの考え方を踏まえ、下の練習問題(大学受験の問題)にチャレンジしましょう!
練習問題(2010大阪大、2015横浜国立大)
【練習①】2010大阪大学(文系の一部)
曲線C:\(y=-x^2-1\) を考える.
\(t\) が実数全体を動くとき,曲線C上の点(\(t\),\(-t^2-1\) を頂点とする放物線
\(y=\displaystyle\frac{3}{4}(x-t)^2-t^2-1\)
が通過する領域を \(xy\) 平面上に図示せよ.
【練習②】2015横浜国立大学
実数 \(a\) に対し,平面上の放物線C:\(y=(x-a)^2-2a^2+1\) を考える.次の問に答えよ.
(1) \(a\) がすべての実数を動くとき,Cが通過する領域を求め,図示せよ.
(2) \(a\) が \(-1≦a≦1\) の範囲を動くとき,Cが通過する領域を求め,図示せよ.
【練習①解答】2010大阪大学
\(y=\displaystyle\frac{3}{4}(x-t)^2-t^2-1\) より
\(t^2+6xt-3x^2+4y+4=0\) ・・・ ①
①が実数解を少なくとも1つ持てばよいので,
\(\displaystyle\frac{(①の判別式)}{4} = (3x)^2-(-3x^2+4y+4)≧0\)
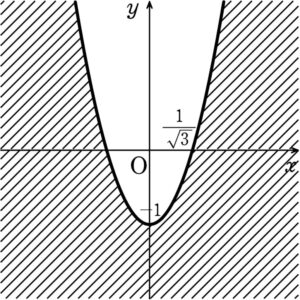
\(y≦3x^2-1\)
したがって求める領域は、右図の斜線部で、境界線を含む.
【練習②解答】2015横浜国立大学
(1) \(y=(x-a)^2-2a^2+1\) より
\(a^2+2xa+y-x^2-1=0\) ・・・ ①
①が実数解を少なくとも1つ持てばよいので,
\(\displaystyle\frac{(①の判別式)}{4} = x^2-( y-x^2-1)≧0\)
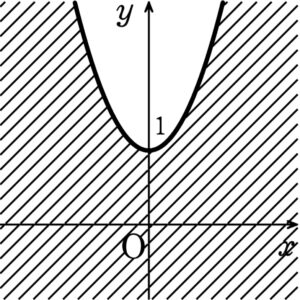
よって\(y≦2x^2+1\)
したがって求める領域は、右図の斜線部で、境界線を含む.
(2) \(f(a)=a^2+2xa+y-x^2-1\) とおく.
\(f(a)=(a+x)^2-2x^2+y-1\)
①が,\(-1≦a≦1\) に少なくとも1つ実数解をもつ条件を考えればよい.
(ⅰ) \(-1≦a≦1\) に2実解(重解を含む)をもつとき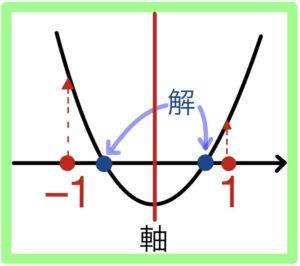
・\((①の判別式)≧0\)
・\(-1≦軸≦1\)
・\(f(-1)≧0\)
・\(f(1)≧0\) を満たせばよい.
それぞれ計算すると
・\(y≦2x^2+1\)
・\(-1≦x≦1\)
・\(y≧(x-1)^2-1\)
・\(y≧(x+1)^2-1\)
(ⅱ) \(-1≦a≦1\) に1実解(重解を除く)をもつとき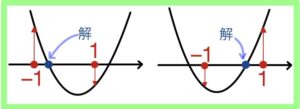
・\(f(-1)≧0\) かつ \(f(1)≦0\)
または
・\(f(-1)≦0\) かつ \(f(1)≧0\)
[ ※ \(f(-1) \times f(1)≦0\) とまとめて処理することが一般的 ]
それぞれ計算すると。
・\(y≧(x-1)^2-1\) かつ \(y≦(x+1)^2-1\)
または
・\(y≦(x-1)^2-1\) かつ \(y≧(x+1)^2-1\)
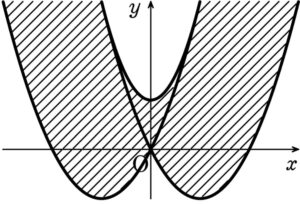
(ⅰ)、(ⅱ)より求める領域は、右図の斜線部で、境界線を含む.









コメント