【2021早稲田大学・商】
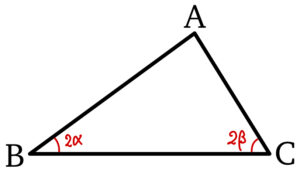
三角形 \(ABC\) において，\(\angle B=2\alpha\)，\(\angle C=2\beta\) とする．
\(\tan\alpha\tan\beta=x\)，\(\displaystyle\frac{AB+AC}{BC}=y\) とするとき，\(y\) を \(x\) で表せ．
三角比や三角関数の公式はただただ覚えるだけではダメです！しっかりと実践問題の中で使えるかどうかがとても大切！そこで，三角比・三角関数のただただ公式を使うだけの問題あるが，差がつく良問を通し，しっかりと演習を行いましょう！
三角関数の公式確認
《加法定理》
・\(\sin(\alpha±\beta)=\sin\alpha \cos\beta±\cos\alpha \sin\beta \)
・\(\cos(\alpha±\beta)=\cos\alpha \cos\beta ∓\sin\alpha \sin\beta \)
・\(\tan(\alpha±\beta)=\displaystyle\frac{\tan\alpha±\tan\beta }{1∓\tan\alpha \tan\beta }\)
《2倍角の公式》
\(\begin{align*} \sin2\alpha &= 2\sin\alpha\cos\alpha \\[5pt] \cos2\alpha &= \cos^2\alpha – \sin^2\alpha \\[5pt] &= 1-2\sin^2\alpha \\[5pt] &= 2\cos^2\alpha -1 \\[5pt] \tan2\alpha &= \frac{2\tan\alpha}{1-\tan^2\alpha} \end{align*}\)
《和積の公式》
\(\begin{align*} \sin \alpha + \sin \beta &= 2\sin\frac{\alpha+\beta}{2} \cos\frac{\alpha-\beta}{2}\\[5pt]\sin \alpha – \sin \beta &= 2\cos\frac{\alpha+\beta}{2} \sin\frac{\alpha-\beta}{2}\\[5pt]\cos \alpha + \cos \beta &= 2\cos\frac{\alpha+\beta}{2} \cos\frac{\alpha-\beta}{2}\\[5pt]\cos \alpha – \cos \beta &= -2\sin\frac{\alpha+\beta}{2} \sin\frac{\alpha-\beta}{2} \\[5pt] \end{align*}\)
解答
\(\triangle ABC\) の外接円の半径を \(R\) とすると，正弦定理より
\(\displaystyle\frac{BC}{\sin\left\{2\pi-(2\alpha+2\beta)\right\}}=\displaystyle\frac{AC}{\sin 2\alpha}=\displaystyle\frac{AB}{\sin 2\beta}=2R\)
よって，
\(BC=2R\sin\left\{2\pi-(2\alpha+2\beta)\right\}=2R\sin2(\alpha+\beta)\)
\(AC=2R\sin2\alpha\)
\(AB=2R\sin2\beta\) より
\(y=\displaystyle\frac{2R\sin2\alpha+2R\sin2\beta}{2R\sin2(\alpha+\beta)}=\displaystyle\frac{\sin2\alpha+\sin2\beta}{\sin2(\alpha+\beta)}\) ・・・①
(分子)は和積の公式
(分母)は2倍角の公式を利用！
ここで，
(分子) \(=2\sin (\alpha+\beta)\cos (\alpha-\beta)\)
(分母) \(=2\sin (\alpha+\beta)\cos (\alpha+\beta)\)
であるから①より
\(y=\displaystyle\frac{\cos (\alpha-\beta)}{\cos (\alpha+\beta)}\)
(分母)，(分子)に加法定理を利用！
\(y=\displaystyle\frac{\cos\alpha\cos\beta+\sin\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}\)
(分母)，(分子)を \(\cos\alpha\cos\beta\) で割る！
\(y=\displaystyle\frac{1+\displaystyle\frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}{1-\displaystyle\frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}=\displaystyle\frac{1+\tan\alpha\tan\beta}{1-\tan\alpha\tan\beta}\)
したがって，\(y=\displaystyle\frac{1+x}{1-x}\)
コメント