【2021 関西医科大学】x^2-| x |y+y^2=3を満たす整数解

2021 関西医科大学［整数問題］

問題文を読んで最初に思うこと

絶対値の処理【その1：\(x^2=| x |^2\)】

\(x^2=| x |^2\) より

\(| x |^2-| x |y+y^2=3\)

\(| x |^2-y| x |+y^2-3=0\)

これが整数解を持つので、実数解を持つと考え、判別式を考えると、

(判別式) \(=(-y)^2-4(y^2-3)≧0\)

よって、\(y^2≦4\)

\(y\) は整数なので、\(y=-2 , -1 , 0 , 1 , 2\)

( ⅰ )　\(y=-2\) のとき

\(| x |^2+2| x |+1=0\)

\((| x |+1)^2=0\)

\(| x |=-1\)

これを満たす整数 \(x\) は存在しないため不適

( ⅱ )　\(y=-1\) のとき

\(| x |^2+| x |-2=0\)

\((| x |+2)(| x |-1)=0\)

\(| x |≧0\) より \(| x |=1\)

よって、\(x=\pm1\)

( ⅲ )　\(y=0\) のとき

\(| x |^2=3\)

これを満たす整数 \(x\) は存在しないため不適

( ⅳ )　\(y=1\) のとき

\(| x |^2-| x |-2=0\)

\((| x |-2)(| x |+1)=0\)

\(| x |≧0\) より \(| x |=2\)

よって、\(x=\pm2\)

( ⅴ )　\(y=2\) のとき

\(| x |^2-2| x |+1=0\)

\((| x |-1)^2=0\)

\(| x |=1\)

\(x=\pm1\)

以上より、求める整数解は

\(( x , y ) = ( -1 , -1 ) , ( 1 , -1 ) , ( -2 , 1 ) , ( 2 , 1 ) , ( -1 , 2 ) , ( 1 , 2 )\)

絶対値の処理【その2：偶関数の利用】

\(x\) に \(-x\) を代入しても元通り

👉 \(y\) 軸に関して対称なグラフ

👉 \(x≧0\) を考えれば良い

参考【愛❤️のある関数】

\(x^2-| x |y+y^2=3\) のグラフは、

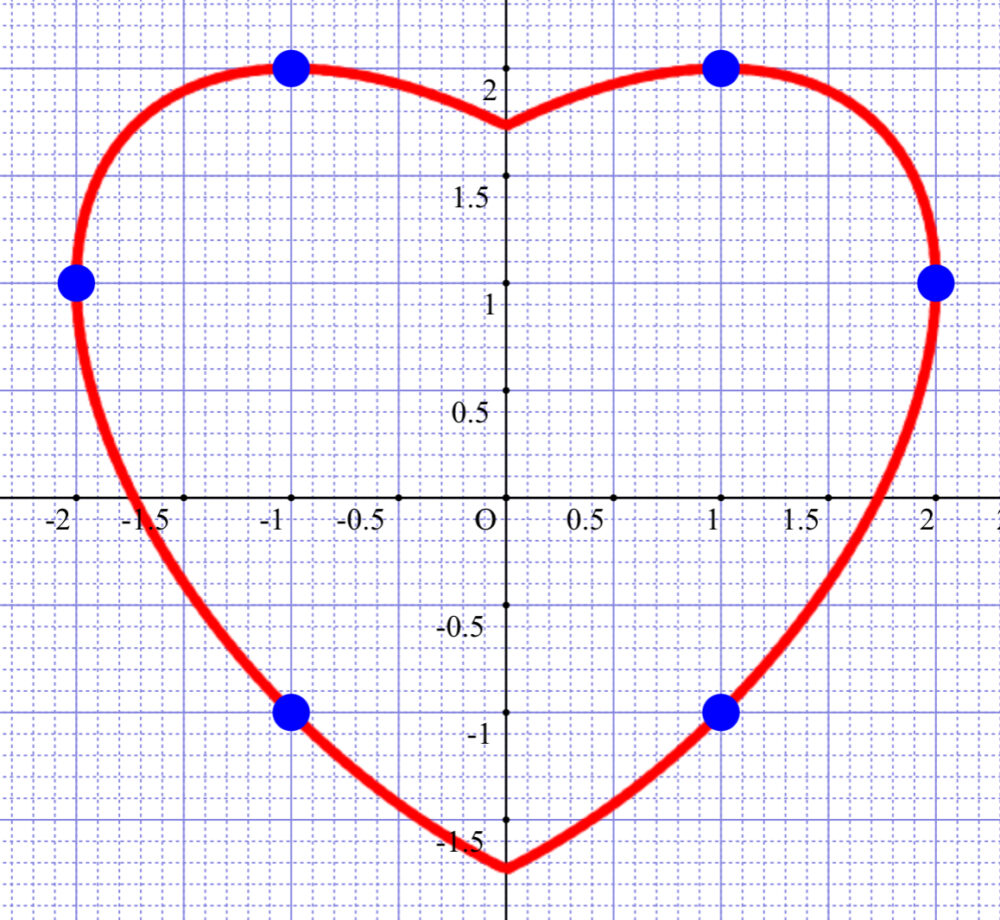
求める整数解は、ハートの格子点ということですね！

なかなかオシャレな問題でした。

他にも整数問題の考え方をたくさん紹介しています。ぜひ受験勉強にお役立てください。

整数問題は大学受験で頻出であるにも関わらず、学校の授業ではあまり学習しません。

有名パターンを一通り勉強したい人はぜひ、下の問題集のどちらか一冊を取り組みましょう！