【2022慶應義塾大学・商学部】
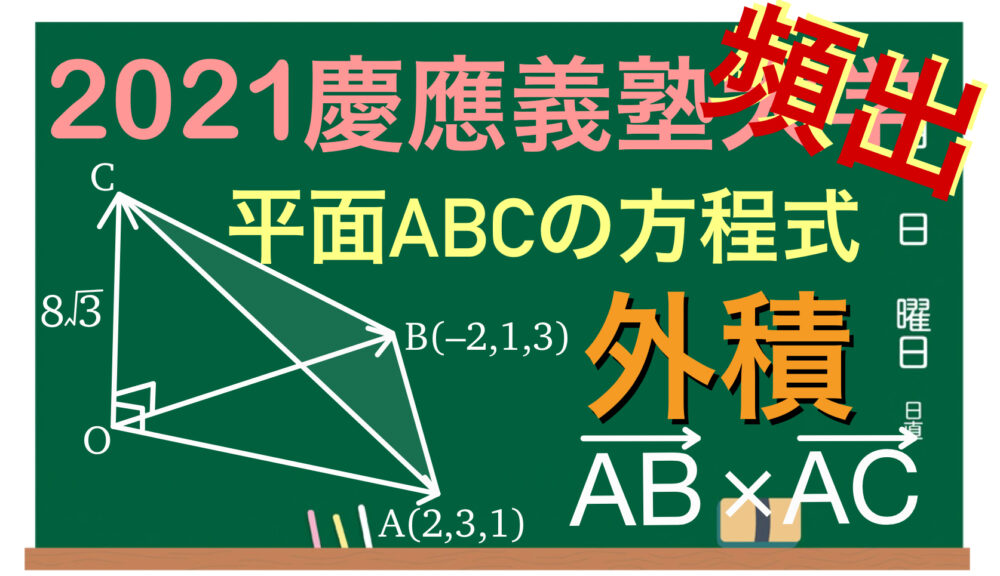
点 \(O\) を原点とする \(xyz\) 座標空間に,\(2\) 点 \(A ( 2 , 3 , 1 )\) , \(B ( -2 , 1 , 3 )\) をとる.また,\(x\) 座標が正の点 \(C\) を,\(\overrightarrow{OC}\) が \(\overrightarrow{OA}\) と \(\overrightarrow{OB}\) に垂直で,\(\left|\overrightarrow{OC}\right|=8\sqrt{3}\) となるように定める.
(1) \(\triangle OAB\) の面積を求めよ.
(2) 点 \(C\) の座標を求めよ.
(3) 四面体 \(OABC\) の体積を求めよ.
(4) 平面 \(ABC\) の方程式を求めよ.
(5) 原点 \(O\) から平面 \(ABC\) に垂線 \(OH\) を下ろしたときの点 \(H\) の座標を求めよ.
(1) 考え方・解答
【重要公式】三角形の面積公式(ベクトル)
(1) 解答
\(\left|\overrightarrow{OA}\right|=\sqrt{2^2+3^2+1^2}=\sqrt{14}\)
\(\left|\overrightarrow{OB}\right|=\sqrt{(-2)^2+1^2+3^2}=\sqrt{14}\)
\(\overrightarrow{OA}\cdot\overrightarrow{OB}=2\times (-2)+3\times 1+1\times 3=2\) より
\(\triangle OAB=\displaystyle\frac{1}{2}\sqrt{\sqrt{14}^2\times \sqrt{14}^2-2^2}=\)\(4\sqrt{3}\)
(2) 考え方・解答
外積の利用
\(\overrightarrow{x}=(a_{1},a_{2},a_{3})\) , \(\overrightarrow{y}=(b_{1},b_{2},b_{3})\) のとき,
\(\overrightarrow{x}\) と \(\overrightarrow{y}\) の両方に垂直なベクトルの1つは
\(\overrightarrow{x}\times \overrightarrow{y}=(a_{2}b_{3}-a_{3}b_{2},a_{3}b_{1}-a_{1}b_{3},a_{1}b_{2}-a_{2}b_{1})\)
※ \(\vec{x}\times\vec{y}\) を \(\vec{x}\) と \(\vec{y}\) の外積という
※ 外積は高校数学では学習しません。(教科書に載っていません)そのため,記述式の答案で使用すると、減点される可能性があります。使用する場合は、記述として解答に残さないこと!本問では私立大学で答えのみで良いので外積を利用しました。
※ 外積を利用した演習として「平面の方程式・点と平面の距離・空間上の直線の方程式・外積の公式まとめ・例題演習」
(2) 解答
\(\overrightarrow{x}\) と \(\overrightarrow{y}\) の両方に垂直なベクトルの1つは,
\(\overrightarrow{OA}\times \overrightarrow{OB}=(8,-8,8)\)
これは \(x\) 座標が正であり,\(\left|\overrightarrow{OA}\times \overrightarrow{OB}\right|=8\sqrt{3}\) となり題意を満たす.
よって,\(\overrightarrow{OC}=(8,-8,8)\)
したがって,点 \(C\) の座標は \(C(8,-8,8)\)
(3) 考え方・解答
体積について
体積について問われたら,まず高さを考える!
高さを考えるためには,2ヶ所垂直になっていることを確認する必要がある
【垂直条件】
平面 \(\alpha\) 上の異なる \(2\) つのベクトル \(\overrightarrow{x}\) , \(\overrightarrow{y}\) ( ただし,\(\overrightarrow{x}\) , \(\overrightarrow{y}\) は零ベクトルでなく,互いに平行ではない ) に対して,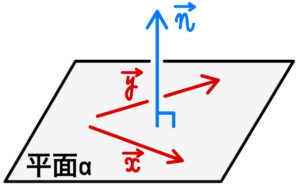
平面 \(\alpha\) \(\perp \overrightarrow{n}\)
\(\iff\) \(\overrightarrow{x} \perp \overrightarrow{n}\) かつ \(\overrightarrow{y} \perp \overrightarrow{n}\)
本問では \(\overrightarrow{OC}\) が \(\overrightarrow{OA}\) と \(\overrightarrow{OB}\) に垂直であるから,線分 \(OC\) が高さとなる.
(3) 解答
求める体積を \(V\) とすると,
\(V=\displaystyle\frac{1}{3}\times \triangle OAB\times \left|\overrightarrow{OC}\right|=\displaystyle\frac{1}{3}\times 4\sqrt{3}\times 8\sqrt{3}=\)\(32\)
(4),(5) 考え方・解答
平面の方程式
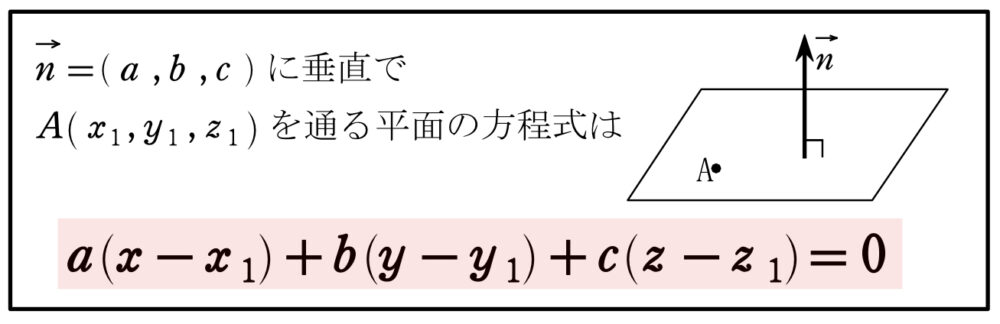
証明・公式の使い方等についての詳細は,「平面の方程式・点と平面の距離・空間上の直線の方程式・外積の公式まとめ・例題演習」を参考にしてください。
(4),(5) 解答
\(\overrightarrow{AB}=(-4,-2,2)\) , \(\overrightarrow{AC}=(6,-11,7)\) より
\(\overrightarrow{AB}\) , \(\overrightarrow{AC}\) の両方に垂直なベクトルの1つは,
\(\overrightarrow{AB}\times \overrightarrow{AC}=(8,40,56)=8(1,5,7)\) より,
\(\overrightarrow{n}=(1,5,7)\) とおくと
平面 \(ABC\) のは,点 \(A ( 2 , 3 , 1 )\) を通り,\(\overrightarrow{n}\) に垂直な平面であるから,
\(1\cdot(x-2)+5\cdot(y-3)+7\cdot(z-1)=0\)
しがたって,\(x+5y+7z-24=0\) ・・・(4)
次に,\(\overrightarrow{OH} \perp \overrightarrow{n}\) であるから,
実数 \(k\) を用いて、\(\overrightarrow{OH}=k\overrightarrow{n}\) とおける.
つまり,\(\overrightarrow{OH}=(k,5k,7k)\)
よって \(H(k,5k,7k)\)
点 \(H\) は,平面 \(ABC\) 上にあるので,
(4)で求めた \(x+5y+7z-24=0\) に代入すると
\(k+25k+49k-24=0\)
\(k=\displaystyle\frac{8}{25}\)
したがって,\(H\left(\displaystyle\frac{8}{25},\displaystyle\frac{8}{5},\displaystyle\frac{56}{25}\right)\)






コメント