【2019東京大学・理】
\(n\) を \(1\) 以上の整数とする.
(1) \(n^2+1\) と \(5n^2+9\) の最大公約数 \(d_{n}\) を求めよ.
(2) \((n^2+1)(5n^2+9)\) は整数の \(2\) 乗にならないことを示せ.
整数問題のPoint
まず整数問題すべてに共通して言えるPointは
- 積の形に変形
- 条件から範囲を絞る
- 倍数や余りに注目
整数問題の多くが、上の1から3のいずれかで処理できます。
この3つのPointは絶対に頭の中に叩き込んでください!
☆平方数・指数はmod 3,4,5,8 が有効
難関大学ではよく出題されるPointの1つ!
まずは下の表を見てください。
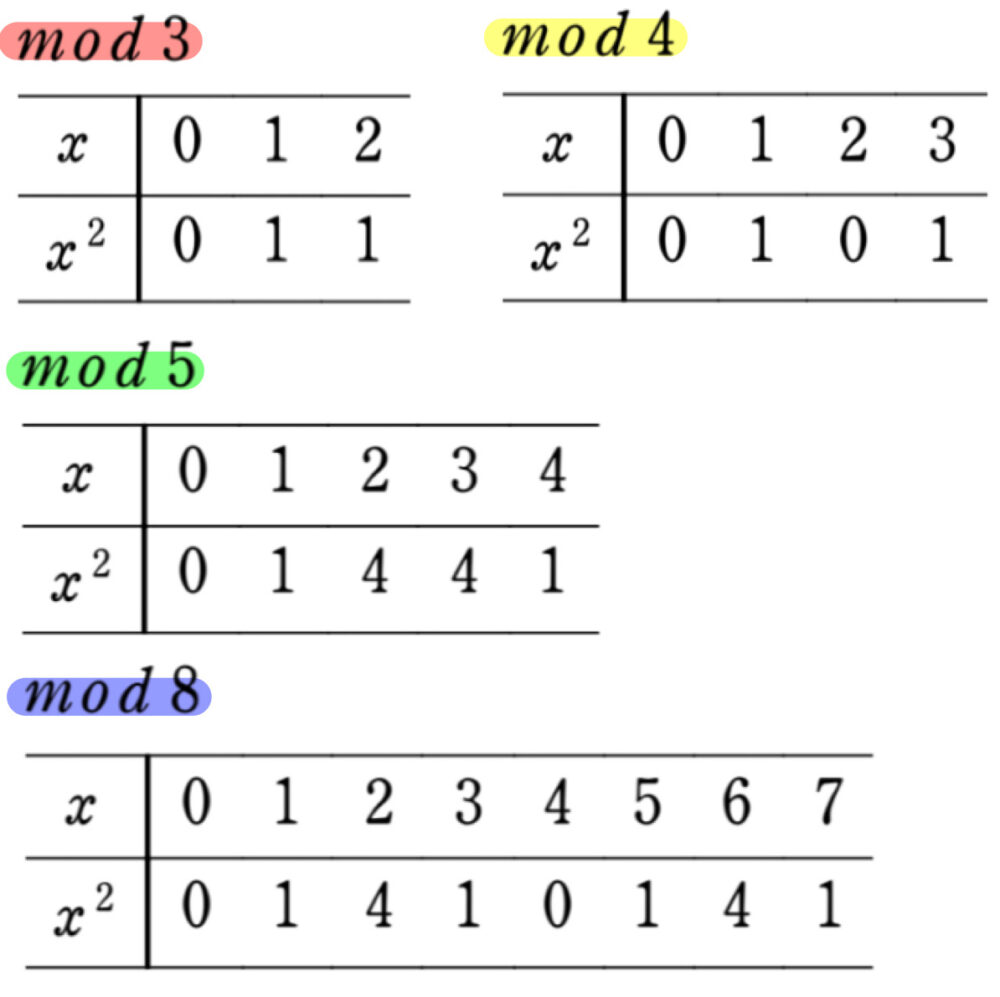
- mod 3 ➡ 「0、1」のみ
- mod 4 ➡ 「0、1」のみ
- mod 5 ➡ 「0、1、4」のみ
- mod 8 ➡ 「0、1、4」のみ
この性質を使って解く演習問題


ユークリッド互除法
【ユークリッドの互除法】
\(2\) つの自然数 \(a\) 、\(b\) において、\(a\) を \(b\) で割ったときの商を \(q\)、余りを \(r\) とすると
\(a\) と \(b\) の最大公約数は、\(b\) と \(r\) の最大公約数に等しい
最大公約数の求め方については様々ありますが、ここではユークリッド互除法を利用した解法を紹介します。


(1) 解答・解説
\(5n^2+9=5(n^2+1)+4\) より
ユークリッド互除法から、
\(5n^2+9\) と \(n^2+1\) の最大公約数は
\(n^2+1\) と \(4\) の最大公約数に等しい.
以下、\(mod 4\) で考えると
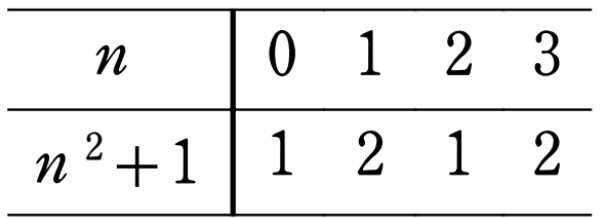
よって、上の表より
(ア) \(n\) が奇数のとき
\(n^2+1≡1\) であるから、\(n^2+1\) と \(4\) の最大公約数 \(d_{n}=1\)
(イ) \(n\) が偶数のとき
\(n^2+1≡2\) であるから、\(n^2+1\) と \(4\) の最大公約数 \(d_{n}=2\)
(2) 解答・解説
\(2\) 乗にならないことを示せ
⇒ \(2\) 乗になると仮定して矛盾を導く(背理法)
\((n^2+1)(5n^2+9)\) が平方数になる・・・① と仮定する.
(ア) \(n\) が奇数のとき
(1)より、\(d_{n}=1\) であるから、
\(n^2+1\) と \(5n^2+9\) は互いに素・・・②
①かつ②より、
\(n^2+1\) と \(5n^2+9\) はともに平方数となる.(※)・・・③
ここで、\(n^2<n^2+1<n^2+2n+1=(n+1)^2\) であるから、
\(n^2+1\) が平方数になることはない.
よって、矛盾する.
(イ) \(n\) が偶数のとき
(1)より、\(d_{n}=2\) であるから
\(n^2+1=2\times \displaystyle\frac{n^2+1}{2}\)
\(5n^2+9=2\times \displaystyle\frac{5n^2+9}{2}\) として、
\(\displaystyle\frac{n^2+1}{2}\)、\(\displaystyle\frac{5n^2+9}{2}\) は互いに素・・・④となる.
\((n^2+1)(5n^2+9)=2^2\times \displaystyle\frac{n^2+1}{2}\times \displaystyle\frac{5n^2+9}{2}\)・・・⑤
①、④、⑤より、(ア)と同様に考え
\(\displaystyle\frac{n^2+1}{2}\)、\(\displaystyle\frac{5n^2+9}{2}\) はともに平方数となる.
ここで、\(n\) は奇数であるから、\(n=2m-1\) ( \(m\) は自然数 )とおくと、
\(\displaystyle\frac{5n^2+9}{2}=10m^2-10m+7=10m(m-1)+7\)
よって、
\(\displaystyle\frac{5n^2+9}{2}=10m(m-1)+7≡2\) ( \(mod 5\) ) となるが、
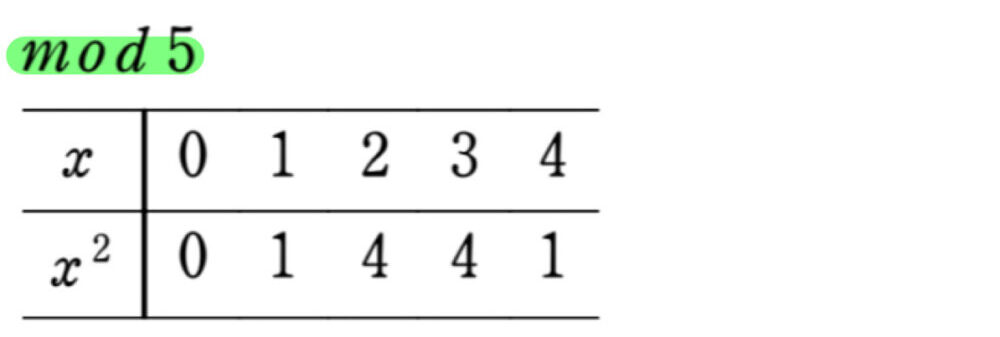
であるから、\(mod 5\) において、\(\displaystyle\frac{5n^2+9}{2}\) は平方数となり得ない.したがってこれは矛盾する.
以上より、
\((n^2+1)(5n^2+9)\) は整数の \(2\) 乗にならない.







コメント