【2012京都大学・文】
次の条件 ( ※ ) を満たす正の実数の組 \((a,b)\) の範囲を求め，座標平面上に図示せよ．
( ※ ) \(\cos a\theta=\cos b\theta\) かつ \(0< \theta≦\pi\) となる \(\theta\) がちょうど \(1\) つある．
1992年に京都大学の過去問で類題が出題されています。数十年おきに出題されているため，そろそろ出題されてもおかしくない？？有名な三角関数の問題ですから，京都大学志望以外の方もしっかりとマスターしておきましょう！
\(\cos A=\cos B\) について
考え方①単位円で考える
\(\cos A=\cos B\)
\(\iff\) \(A=\pm B+2n\pi\) ( \(n\) は整数 )
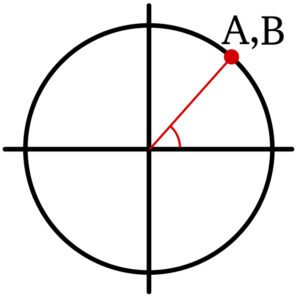《単位円で \(A\) と \(B\) が同じ位置にあるとき》
一番シンプルなのは \(A=B\) ( \(n=0\) のとき )
他にも， \(A\) が \(B\) よりも一周分 ( 2 \(\pi\) 分 ) だけ大きい角度であるとき
\(A=B+2\pi\) ( \(n=1\) のとき )
というように， \(A\) と \(B\) が同じ位置にいるとき， \(A=B+2n\pi\) の関係が成り立つ，
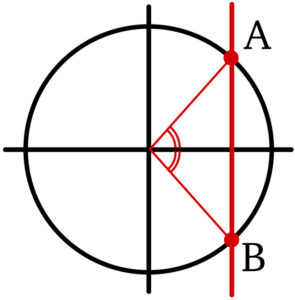《単位円で \(x\) 座標が同じ(異なる点)のとき》
例えば，\(\cos 60°=\cos 300°\) のように，
\(60°+300°=360° ( 2\pi )\) ( \(n=0\) ) のときに成り立つ．
他にも，\(\cos 60°=\cos (60°+360°\times n)\) であるから
\(\cos (60°+360°\times n)=\cos 300°\) となり，
\((60°+360°\times n)+300°=360°+360°\times n ( =2\pi+2n\pi)\) の関係が成り立つ．
よって， \(A\) と \(B\) の \(x\) 座標が同じとき， \(A+B=2\pi+2n\pi\)
つまり \(A=-B+2\pi+2n\pi\) の関係が成り立つ，
考え方②和積の公式の利用
和積の公式
\(\cos A-\cos B=-2\sin\displaystyle\frac{A+B}{2}\sin\displaystyle\frac{A-B}{2}\)
※その他，三角関数に関する公式まとめは「【三角関数】公式まとめ&差がつく入試問題演習」
解答・解説
解答①
\(\cos a\theta=\cos b\theta\) ・・・①
\(a=b\) のとき，①はすべての \(\theta\) で成り立つため ( ※ ) を満たさない．
( ⅰ ) \(0<b<a\) のとき
\(m\) , \(n\) を整数として
① \(\iff\) \(a\theta=b\theta+2m\pi\) または \(a\theta=-b\theta+2n\pi\)
よって，
\(\theta=\displaystyle\frac{2m}{a-b}\pi\) ・・・②
\(\theta=\displaystyle\frac{2n}{a+b}\pi\) ・・・③
②のうち，正の解を小さい順に並べると
\(\theta=\displaystyle\frac{2}{a-b}\pi , \displaystyle\frac{4}{a-b}\pi , \displaystyle\frac{6}{a-b}\pi , \cdots\)
③のうち，正の解を小さい順に並べると
\(\theta=\displaystyle\frac{2}{a+b}\pi , \displaystyle\frac{4}{a+b}\pi , \displaystyle\frac{6}{a+b}\pi , \cdots\)
これらの中で最小のものは，\(\displaystyle\frac{2}{a+b}\pi\) であるから
( ※ ) を満たすのは
\(\begin{cases}0<\displaystyle\frac{2}{a+b}\pi≦\pi\\\pi<\displaystyle\frac{4}{a+b}\pi\\\pi<\displaystyle\frac{2}{a-b}\pi\end{cases}\)
\(\iff\) \(\begin{cases}2≦a+b<4\\a-b<2\end{cases}\)
( ⅱ ) \(0<a<b\) のとき
( ⅰ ) と同様に考え，\(\begin{cases}2≦a+b<4\\b-a<2\end{cases}\)
したがって，求める \((a,b)\) の範囲は
\(\begin{cases}0<b<a\\2≦a+b<4\\b>a-2\end{cases}\)
または
\(\begin{cases}0<a<b\\2≦a+b<4\\b<a+2\end{cases}\)
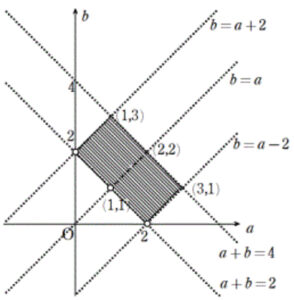これを図示すると，右の図の斜線部となる．
ただし，境界線上のうち実線は含み，点線は含まない
また，\(2\) 点 \((2,0)\) , \((0,2)\) と直線 \(b=a\) 上の点は含まない
解答②(途中まで)
\(\cos a\theta=\cos b\theta\) より
\(\cos a\theta-\cos b\theta=0\)
和積の公式から
\(\cos a\theta-\cos b\theta=-2\sin\displaystyle\frac{a+b}{2}\theta\sin\displaystyle\frac{a-b}{2}\theta=0\)
\(\sin\displaystyle\frac{a+b}{2}\theta=0\) または \(\sin\displaystyle\frac{a-b}{2}\theta=0\)
整数 \(m\) , \(n\) を用いて
\(\displaystyle\frac{a+b}{2}\theta=n\pi\) または \(\displaystyle\frac{a-b}{2}\theta=m\pi\)
※以下は解法①のと同様のため省略
コメント