【問題11】2000 名古屋市立大学
\(2\) つの複素数 \(z\) と \(w\) との間に、\(w=\displaystyle\frac{z+i}{z+1}\) なる関係がある.
ただし、\(z+1\not=0\) とする.
(1) \(z\) が複素数平面上の虚軸を動くとき、\(w\) の軌跡を求め、図示せよ.
(2) \(z\) が複素数平面上の原点を中心とする半径 \(1\) の円周上を動くとき、\(w\) の軌跡を求めよ.
ここでは、数学Ⅲで学習する複素数平面について、実践問題(入試問題)を使って、ポイント(考え方)まとめをしていきます。
正直に言いますと、教科書をやっただけでは、入試レベルの問題に対応するのは難しいです。
ですから、教科書と入試レベルの橋渡しとして、過去に出題された入試問題を例に、複素数平面においておさえておきたい(入試でよく出る考え方)をまとめていきます。
基本的な考え方をしっかりと身に付け、2次試験で得点源にできるようにしていきましょう!
考え方・確認事項
(1) \(z\) が虚軸上
\(z\) が虚軸上
\(\iff z\) は純虚数 または \(z=0\)
\(\iff ( \overline{z}=-z , z\not=0 )\) または \(z=0\)
\(\iff z+\overline{z}=0\)
(2) \(z\) が原点を中心とする半径 \(1\) の円周上
\(z\) が原点を中心とする半径 \(1\) の円周上を動く
\(\iff | z | =1\)
軌跡の求め方
方針 Ⅰ :条件式から、求める軌跡の文字のみの式に変形
方針Ⅱ :どのような図形になるか直接とらえる
方針 Ⅰ について
まず初めに、\(w=\displaystyle\frac{z+i}{z+1}\) から \(z=(wの式)\) を作り、
\(z\) が虚軸上 \(\iff z+\overline{z}=0\) に代入して \(w\) の式をまとめる
方針Ⅱについて
《例1》定点 \(A\) から距離が \(3\) となる点の軌跡
⇒ \(A\) を中心とする、半径 \(3\) の円
《例2》\(2\) 定点 \(A\)、\(B\) から距離が等しい点の軌跡
⇒ 線分 \(AB\) の垂直二等分線
《例3》\(2\) 定点 \(A\)、\(B\) から距離の比が \(m : n\) となる点の軌跡
⇒ アポロニウスの円
などなど、計算せずとも図形の形を直接捕まえることが出来る.
本問においては、解法②にて紹介.
(1) 解法①:条件式から、求める軌跡の文字のみの式に変形
\(w=\displaystyle\frac{z+i}{z+1}\) より、
\((z+1)w=(z+i)\)
\(z\) についてまとめると、
\((w-1)z=-w+i\) ・・・①
①において、\(w=1\) とすると、
\(0\cdot z=-1+i\) となり不成立.
よって \(w\not=1\) であるから①より
\(z=\displaystyle\frac{-w+i}{w-1}\) ・・・②
また、\(z\) が複素数平面上の虚軸を動くとき
\(z+\overline{z}=0\) より、②を代入すると
\(\displaystyle\frac{-w+i}{w-1}+\overline{\left(\displaystyle\frac{-w+i}{w-1}\right)}=0\)
\(\displaystyle\frac{-w+i}{w-1}+\displaystyle\frac{-\overline{w}-i}{\overline{w}-1}=0\)
\((-w+i)(\overline{w}-1)+(w-1)(-\overline{w}-i)=0\)
展開して式を整理すると、
\(w\overline{w}-\displaystyle\frac{1-i}{2}w-\displaystyle\frac{1+i}{2}\overline{w}=0\)
\(\left(w-\displaystyle\frac{1+i}{2}\right)\left(\overline{w}-\displaystyle\frac{1-i}{2}\right)=\displaystyle\frac{1+i}{2}\cdot\displaystyle\frac{1-i}{2}\)
\(\left(w-\displaystyle\frac{1+i}{2}\right)\overline{\left(w-\displaystyle\frac{1+i}{2}\right)}=\displaystyle\frac{1}{2}\)
以上より、
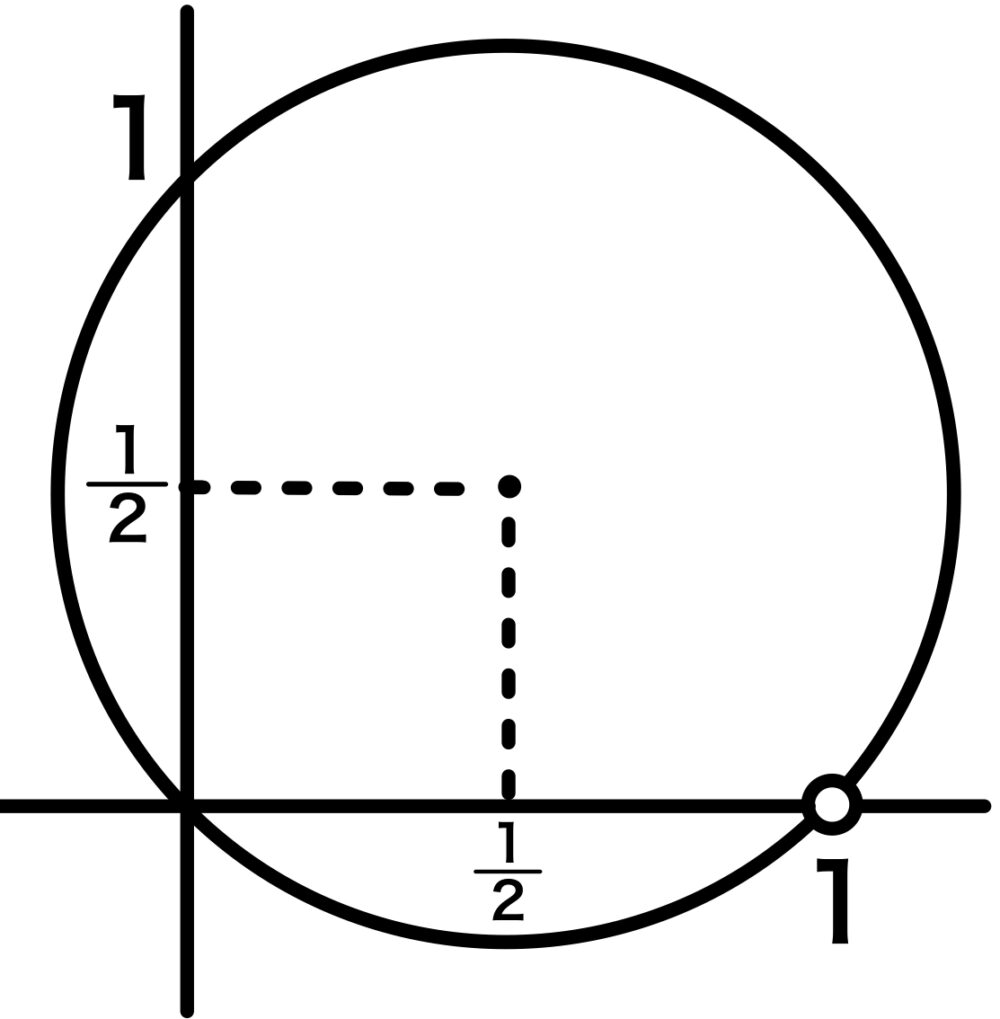
\(\left| w-\displaystyle\frac{1+i}{2} \right|=\displaystyle\frac{1}{\sqrt{2}}\) かつ \(w\not=1\)
図示すると、以下のようになる
(1) 解法②:どのような図形になるか直接とらえる
(1)解法Ⅰの \(z=\displaystyle\frac{-w+i}{w-1}\) ・・・② (\(w\not=1\))
までは同じ.
\(z\) は虚軸上、つまり \(z\) 純虚数または \(0\) なので、
( \(2\) 点 \(w\)、\(1\) を結ぶ線分 ) ⊥ ( \(2\) 点 \(w\)、\(i\) を結ぶ線分 )
ただし \(w\not=1\)
下図より、\(w\) の軌跡は、
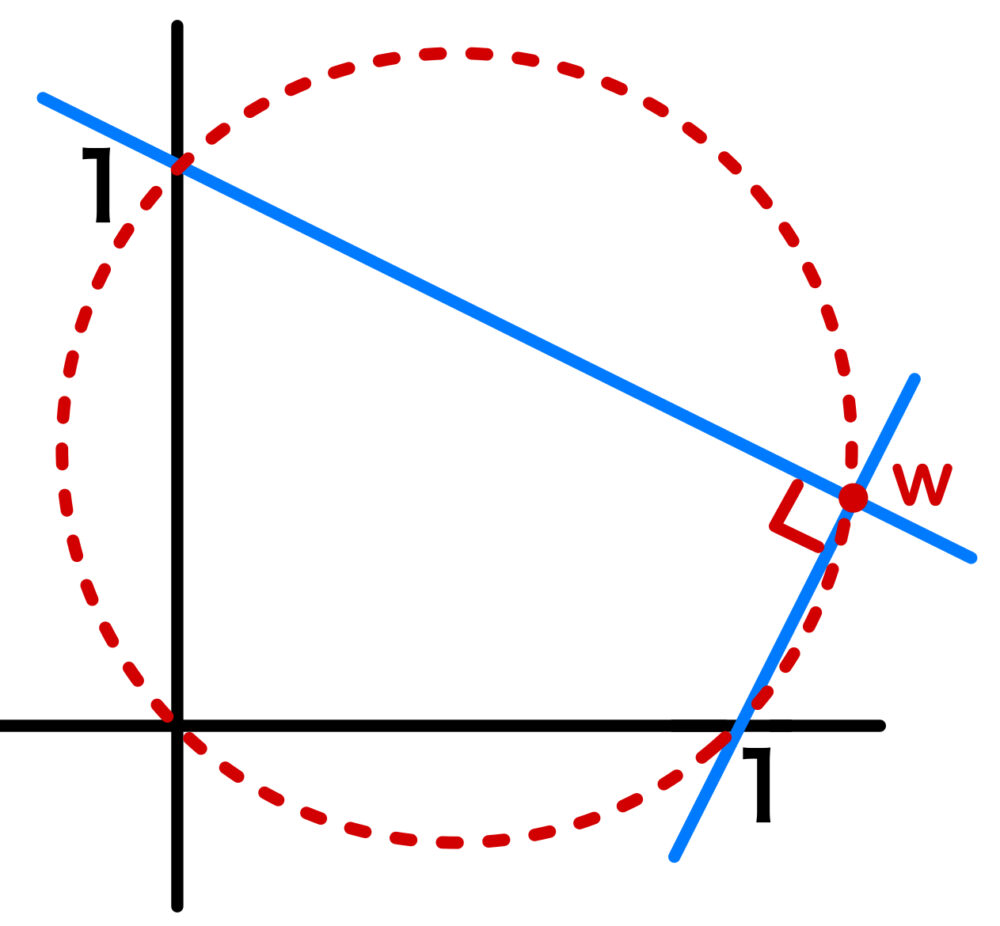
\(2\) 点 \(1\)、\(i\) を直径とする円上で、\(w=1\) を除く
(2) 解答
\(| z |=1\) より、(1)の②を代入して、
\(| \displaystyle\frac{-w+i}{w-1} |=1\)
\(| w-i |=| w-1 |\)
これは、\(w\) が \(2\) 点 \(1\)、\(i\) から距離が等しい点の軌跡を表すので、
求める軌跡は、\(2\) 点 \(1\)、\(i\) を結ぶ線分の垂直二等分線









コメント