【2018九州大学・理・第4問】
整数 \(a\)、\(b\) は \(3\) の倍数でないとし、
\(f(x)=2x^3+a^2x^2+2b^2x+1\) とおく.以下の問いに答えよ.
(1) \(f(1)\) と \(f(2)\) を \(3\) で割った余りをそれぞれ求めよ.
(2) \(f(x)=0\) を満たす整数 \(x\) は存在しないことを示せ.
(3) \(f(x)=0\) を満たす有理数 \(x\) が存在するような組 \((a,b)\) をすべて求めよ.
(1)平方数・指数はmod 3,mod 4 が有効
(1)において、\(f(1)=a^2+2b^2+3\)、\(f(2)=4a^2+4b^2+17\) となり、
\(a^2\)、\(b^2\) (平方数)が共に現れる.
ここで、整数問題を扱う上ではよく出題されるPointの1つ!
まずは下の表を見てください。
平方数において
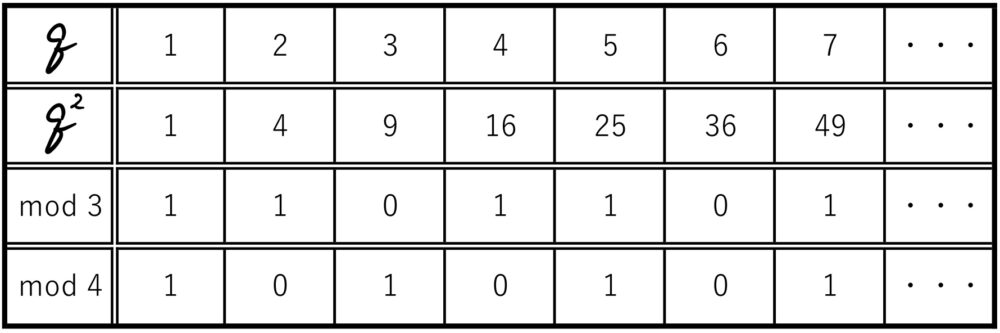
何かの2乗(平方数)において、
mod 3→「1,1,0」の繰り返し
mod 4→「1,0」の繰り返し
という規則が存在!
指数に関しても、同様に考えると規則を持つことが確認できる。
詳しくは類題として「2021 兵庫県立大学【整数】平方数には合同式(mod)を使え!」を参考にしてください。
また、合同式をまだ学習していない、または不安と言う人は、
で合同式をマスターしよう!
整数問題において、合同式が使えないのは致命的です・・・。
合同式は整数問題を扱う上で必須アイテム!しっかりとマスターしておきましょう!
参考:平方数とmod 3、4、5、8について
上で紹介したように、平方数と合同式は非常に相性抜群です!
特に \(mod 3\) や \(mod 4\) は頻出ですので絶対に抑え、さらに参考として、\(mod 5\)、\(mod 8\) についても 紹介しておきます。
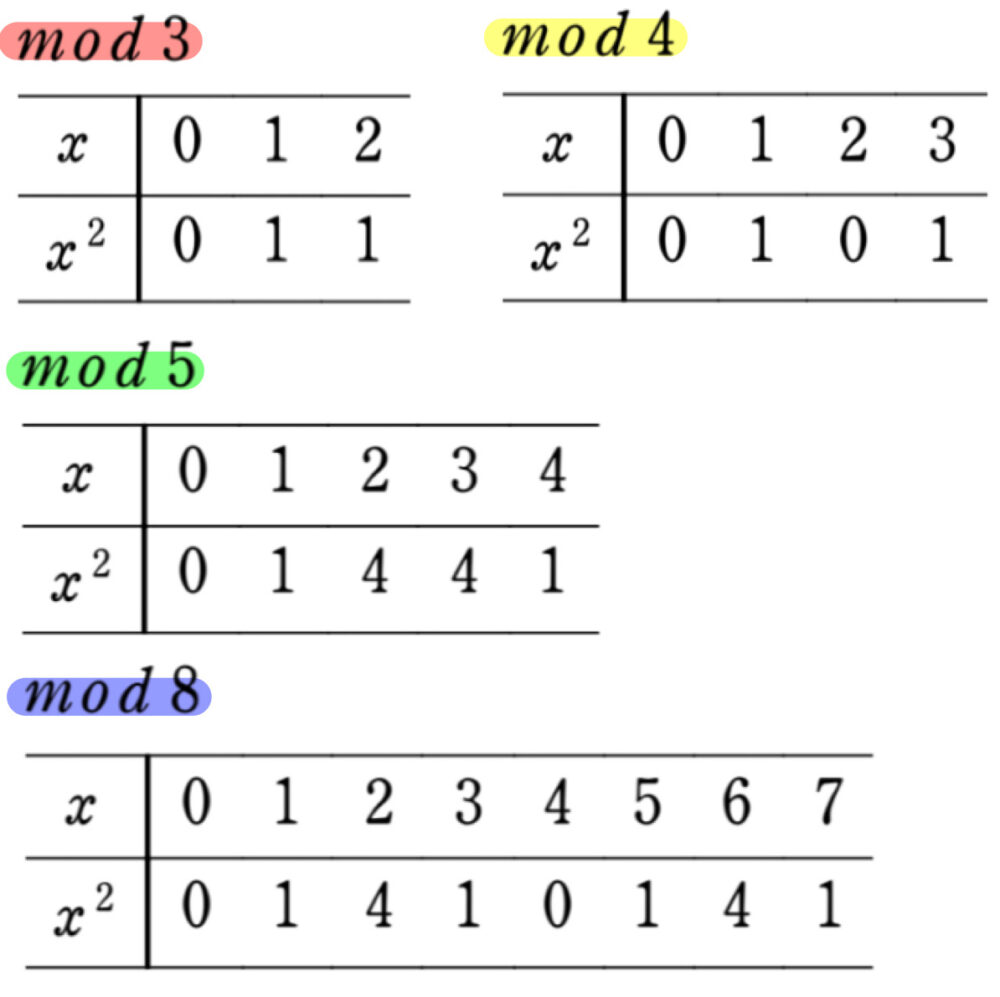
- mod 3 ➡ 「0、1」のみ
- mod 4 ➡ 「0、1」のみ
- mod 5 ➡ 「0、1、4」のみ
- mod 8 ➡ 「0、1、4」のみ
(1)解答
【2018九州大学・理・第4問】
整数 \(a\)、\(b\) は \(3\) の倍数でないとし、
\(f(x)=2x^3+a^2x^2+2b^2x+1\) とおく.以下の問いに答えよ.
(1) \(f(1)\) と \(f(2)\) を \(3\) で割った余りをそれぞれ求めよ.
以下、\(mod3\) として考える.
\(a\)、\(b\) は \(3\) の倍数でない整数であるから、
\(a≡\pm1\)、\(b≡\pm1\) であるため、
\(a^2≡1\)、\(b^2≡1\) となる.
このとき、
\(f(1)=a^2+2b^2+3≡1+2\times1+0≡0\)
\(f(2)=4a^2+4b^2+17≡4\times1+4\times1+2≡1\) であるから、
\(f(1)\)、\(f(2)\) を \(3\) で割った余りは順に、\(0\)、\(1\)
(2)解答[背理法の利用]
【2018九州大学・理・第4問】
整数 \(a\)、\(b\) は \(3\) の倍数でないとし、
\(f(x)=2x^3+a^2x^2+2b^2x+1\) とおく.以下の問いに答えよ.
(1) \(f(1)\) と \(f(2)\) を \(3\) で割った余りをそれぞれ \(0\)、\(1\) とわかった.
(2) \(f(x)=0\) を満たす整数 \(x\) は存在しないことを示せ.

存在しないことの証明は、背理法を利用することが多い!
存在すると仮定して、矛盾を導きましょう!
\(f(x)=0\) を満たす整数 \(x\) が存在すると仮定する.
このとき、\(n\) を整数とすると、
\(f(n)=0\) \(\iff\) \(2n^3+a^2n^2+2b^2n+1=0\) ・・・①
①より
\(n(2n^2+a^2n+2b^2)=-1\) ・・・②
\(a\)、\(b\)、\(n\) は整数であるから、\(n=\pm1\)

( ⅰ ) \(n=1\) のとき
①より、\(a^2+2b^2+3=0\) となるが、
左辺に注目すると、\(a^2+2b^2+3>0\) であるため、これは不適である.
( ⅱ ) \(n=-1\) のとき
①より、\(a^2-2b^2-1=0\)
ここで、左辺を \(3\) で割った余りに注目する( \(mod3\) で考える )と、
\(a^2≡1\)、\(b^2≡1\) であるから、
\(a^2-2b^2-1≡1-2\times1-1=-2≡1\) となり、これは不適である.
したがって、\(f(x)=0\) を満たす整数 \(x\) は存在しない
(3)解答
【2018九州大学・理・第4問】
整数 \(a\)、\(b\) は \(3\) の倍数でないとし、
\(f(x)=2x^3+a^2x^2+2b^2x+1\) とおく.以下の問いに答えよ.
(1) \(f(1)\) と \(f(2)\) を \(3\) で割った余りをそれぞれ \(0\)、\(1\) とわかった.
(2) \(f(x)=0\) を満たす整数 \(x\) は存在しないことを示した.
(3) \(f(x)=0\) を満たす有理数 \(x\) が存在するような組 \((a,b)\) をすべて求めよ.

有理数と言われたら、まずは初期設定はこれでしょう!
任意の有理数 \(\displaystyle\frac{q}{p}\) とおく.
ただし、\(p\)、\(q\) は互いに素な整数で、\(p≧1\) とする.
(2)より、\(f(x)=0\) を満たす整数 \(x\) は存在しないため、\(p=1\) のときは不適である.
つまり、\(p≧2\) の整数とおける.このとき、
\(f\left(\displaystyle\frac{q}{p}\right)=0\) とすると、
\(2\left(\displaystyle\frac{q}{p}\right)^3+a^2\left(\displaystyle\frac{q}{p}\right)^2+2b^2\left(\displaystyle\frac{q}{p}\right)+1=0\)
式を整理すると、
\(2q^3=-p(a^2q^2+2b^2pq+p^2)\) ・・・③
\(p\) は \(2q^3\) の約数であるが、\(p\)、\(q\) は互いに素な整数で、\(p≧2\) であるため、\(p=2\) となる.
③より、
\(2q^3=-2(a^2q^2+4b^2q+4)\)
\(q^3=-a^2q^2-4b^2q-4\)
\(4=-q(q^2+a^2q+4b^2)\)・・・④
④より、 \(q\) は \(4\) の約数で、\(p(=2)\) とは互いに素な整数であるから、\(q=\pm1\)
(ア) \(q=1\) のとき
④より、\(a^2+4b^2+5=0\) となるが、\(a^2+4b^2+5>0\) であるため不適である.
(イ) \(q=-1\) のとき
④より、\(-a^2+4b^2-3=0\)
\((2b+a)(2b-a)=3\)
\((2b+a,2b-a)=(3,1) , (1,3) , (-3,-1) , (-1,-3)\)
したがって、\((a,b)=(1,1),(-1,1),(-1,-1),(1,-1)\)
最後に
(3)については正直難しいです。
ただ(1)、(2)については整数問題の中ではよく出題される典型問題ですから、しっかりと得点できるようにしておきましょう!
(3)については最後まで解けなくても、初期設定など、部分点を取ることができれば、十分に合格ラインは超えられます!
整数問題は、経験の差が合否の差としてはっきりと出てきます。このブログでは、授業(教科書)ではあまり扱わないが、入試では頻出の整数問題を中心に、差がつく分野を取り扱っています。
塾に通っていない、整数問題を武器にしたい受験生は是非他の記事も参考に、整数問題を得意分野にしてください!







コメント