【2019早稲田大学・先進理工】(一部のみ)
自然数 \(n\) について次のような命題を考える．
(※) \(n^2+1\)、\(2n^2+3\)、\(6n^2+5\) がすべて素数である
(※)を満たすような \(n\) は \(n=1 , 2 \) のみであることを示せ．
実際は(１)、(２)と誘導形式の問題であり、考え方、方針の立て方を学習するために、あえて(１)をなくした(２)のみを扱います。
考え方・方針の立て方
整数問題の極意は実験
整数問題の極意は実験することです。
実験を通して、規則や法則を見つけ、解答を作成する方針を考えていきましょう。
具体的に実験
下記の表は、\(n\) に \(1 , 2 , \cdots , 7\) まで具体的に代入したものです。
さらに本問では「素数」かどうかが重要になりますので、素数かどうかを確認するために、素数以外の数はすべて素因数分解を与えています。(空欄のところは素数と言うこと．)
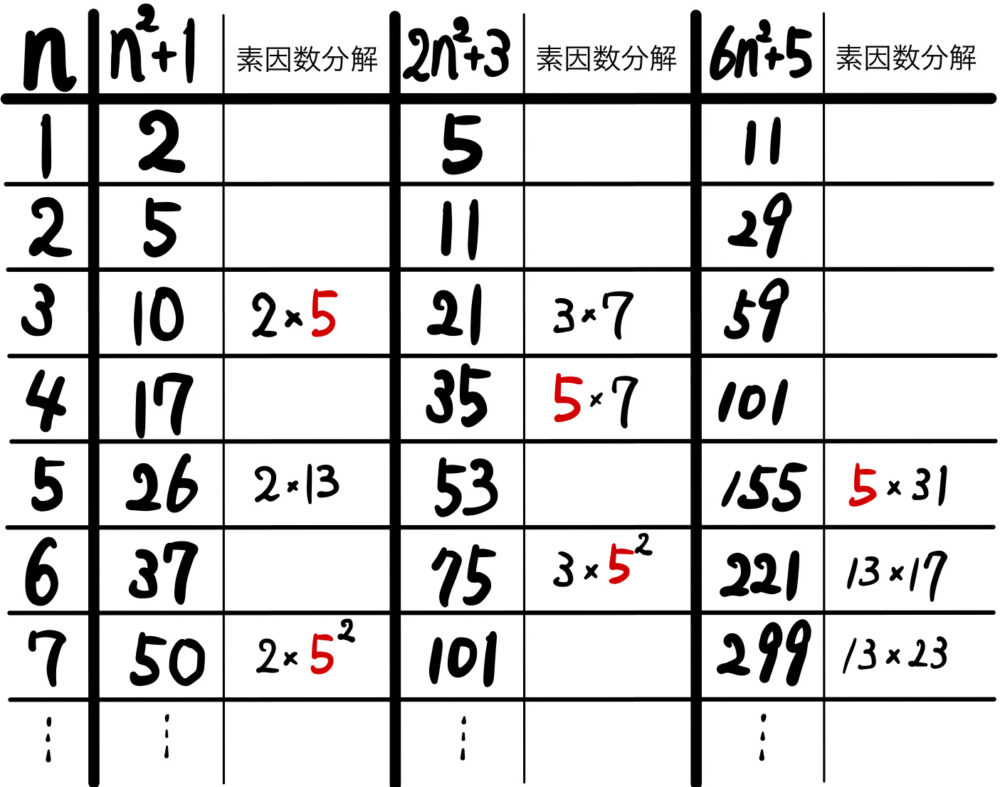
本問では \(n≧3\) においては、\(n^2+1\)、\(2n^2+3\)、\(6n^2+5\) がすべて素数になることがないはずですから、それぞれを素因数分解した値に注目して、規則や法則を考えてみました。
このとき、\(n≧3\) において、\(n^2+1\)、\(2n^2+3\)、\(6n^2+5\) のいずれかは \(5\) の倍数になりそう？？という予想を立てることが出来ます。
そこで、『 mod 5 』で考えてて解答を作成してみようと思います。
※以下では合同式を利用して解答を作成します。
合同式が不安、学習していない人は、
を参考にしてください。整数問題で合同式は必須アイテムです。しっかりと使えるように演習をしておきましょう！
解答
・\(n=1\) のとき
\(n^2+1\)、\(2n^2+3\)、\(6n^2+5\) はそれぞれ、
\(2\)、\(5\)、\(11\) となりすべて素数であるから条件を満たす．
・\(n=2\) のとき
\(n^2+1\)、\(2n^2+3\)、\(6n^2+5\) はそれぞれ、
\(5\)、\(11\)、\(29\) となりすべて素数であるから条件を満たす．
・\(n≧3\) のとき
\(n^2+1\)、\(2n^2+3\)、\(6n^2+5\) はすべて \(5\) より大きい自然数となる・・・①
ここで、以下すべて mod 5 として考える．
(ⅰ) \(n≡0\) のとき
\(6n^2+5≡5≡0\)
(ⅱ) \(n≡\pm1\) のとき
\(2n^2+3≡5≡0\)
(ⅲ) \(n≡\pm2\) のとき
\(n^2+1≡5≡0\)
したがって、①と(ⅰ)～(ⅲ)より、\(n≧3\) において
\(n^2+1\)、\(2n^2+3\)、\(6n^2+5\) のいずれかは \(5\) より大きい \(5\) の倍数となり素数とならない．
したがって、(※)を満たす \(n=1 , 2\) のみである．
\(5\) の倍数になると言っただけでは、\(5\) の倍数で唯一の素数である \(5\) の可能性があるため解答としては不十分．そこで「 \(5\) より大きい \(5\) の倍数」という解答とした．
実際の問題
【2019早稲田大学・先進理工】(一部のみ)
自然数 \(n\) について次のような命題を考える．
(※) \(n^2+1\)、\(2n^2+3\)、\(6n^2+5\) がすべて素数である
(１) \(n=5k\) ( \(k\) は自然数 ) のとき、\(n\) は(※)を満たさないことを示せ．
(２) (※)を満たすような \(n\) は \(n=1 , 2 \) のみであることを示せ．
今回は誘導の(１)をあえてなくしたため、少し難しかったかもしれません。
ちなみに(１)で \(5\) の倍数に注目させていることから、mod 5 への発想を持ってほしいと言う作問者の意図だと感じ取れます。
しかし誘導がなくても、実験から規則を見つけることで方針を見出すことが出来る問題です。
しっかりと手を動かし、何かしらの規則や法則が隠れていますので、その法則を見つけ出す練習を行っていくことで、整数問題は得意分野にできます。ただただ解答をなぞって分かった気になる無意味な学習をやめ、整数問題の正しい考え方を身に付け、整数問題を武器にして他の受験生と差を付けましょう！
このブログでは、他にもたくさん(受験生が苦手とする)整数問題や確率の問題を考え方を中心に扱っています。他の問題を通して演習を行って見て下さい！
コメント