【ベクトルまとめ】おさえておきた入試頻出・重要問題

【2021神戸大学(理)】

$\overrightarrow{0}$ でない $2$ つのベクトル $\overrightarrow{a}$ , $\overrightarrow{b}$ が垂直であるとする．$\overrightarrow{a}+\overrightarrow{b}$ と $\overrightarrow{a}+3\overrightarrow{b}$ のなす角を $\theta$ ( $0≦\theta≦\pi$ ) とする．以下の問に答えよ．

(１)　$\left|\overrightarrow{a}\right|=x$ , $\left|\overrightarrow{b}\right|=y$ とするとき，$\sin^2 \theta$ を $x$ , $y$ を用いて表せ．

(２)　$\theta$ の最大値を求めよ．

【2021京都大学・文】

$\triangle 0AB$ において，$OA=3$ , $OB=2$ , $\angle AOB=60°$ とする．$\triangle OAB$ の垂心 $H$ とするとき，$\overrightarrow{OH}$ を $\overrightarrow{OA}$ と $\overrightarrow{OB}$ を用いて表せ．

【オイラー直線】

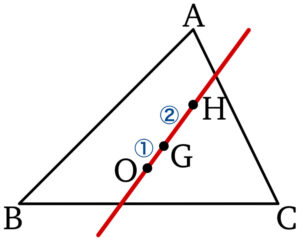
任意の三角形の外心を $O$ , 重心を $G$ , 垂心を $H$ とおくとき,

$3$ 点 $O$ ,  $G$ ,  $H$ は一直線上にある．

また，$OG:GH=1:2$ を満たす．

【2013京都大学(文理共通)】

平行四辺形 $ABCD$ において，辺 $AB$ を $1 : 1$ に内分する点を $E$，辺 $BC$ を $2 : 1$ に内分する点を $F$，辺 $CD$ を $3 : 1$ に内分する点を $G$ とする．線分 $CE$ と線分 $FG$ の交点を $P$ とし，線分 $AP$ を延長した直線と辺 $BC$ の交点を $Q$ とするとき，比 $AP : PQ$ を求めよ．

【問題(4STEP数B125)】

四面体 $OABC$ の辺 $OA$ の中点を $M$ , 辺 $BC$ を $2 : 1$ に内分する点を $Q$ , 線分 $MQ$ の中点を $R$ とし，直線 $OR$ と平面 $ABC$ の交点を $P$ とする．$\overrightarrow{OA}=\overrightarrow{a}$ , $\overrightarrow{OB}=\overrightarrow{b}$ , $\overrightarrow{OC}=\overrightarrow{c}$ とするとき，$\overrightarrow{OP}$ を $\overrightarrow{a}$ , $\overrightarrow{b}$ , $\overrightarrow{c}$ を用いて表せ．

【2016神戸大学・文理(一部)】

四面体 $OABC$ において，$P$ を辺 $OA$ の中点，$Q$ を辺 $OB$ を $2 : 1$ に内分する点，$R$ を辺 $BC$ の中点とする．$P$ , $Q$ , $R$ を通る平面と辺 $AC$ の交点を $S$ とする．$\overrightarrow{OA}=\overrightarrow{a}$ , $\overrightarrow{OB}=\overrightarrow{b}$ ,$\overrightarrow{OC}=\overrightarrow{c}$ とおく．以下の問に答えよ．

(１)　$\overrightarrow{PQ}$ , $\overrightarrow{PR}$ をそれぞれ $\overrightarrow{OA}=\overrightarrow{a}$ , $\overrightarrow{OB}=\overrightarrow{b}$ ,$\overrightarrow{OC}=\overrightarrow{c}$ を用いて表せ．

(２)　比 $\left|\overrightarrow{AS}\right| : \left|\overrightarrow{SC}\right|$ を求めよ．

$4$ 点 $O ( 0 , 0 , 0 )$ ,  $A ( 1 , 2 , 0 )$ ,  $B ( 3 , 0 , 4 )$ ,  $C ( 0 , 1 , 1 )$ がある．

四面体 $OABC$ の体積を求めよ．

【2010神戸大学・文(一部)】

空間内に $4$ 点 $O$ , $A$ , $B$ , $C$ があり，

$OA=3$ , $OB=OC=4$ , $\angle BOC=\angle COA=\angle AOB=\displaystyle\frac{\pi}{3}$

であるとする．$3$ 点 $A$ , $B$ , $C$ を通る平面に垂線 $OH$ をおろす．

$\overrightarrow{a}=\overrightarrow{OA}$ , $\overrightarrow{b}=\overrightarrow{OB}$ , $\overrightarrow{c}=\overrightarrow{OC}$ とし，

$\overrightarrow{OH}=r\overrightarrow{a}+s\overrightarrow{b}+t\overrightarrow{c}$

と表すとき， $r$ , $s$ , $t$ を求めよ．

【2004京都大学(文)】

$\triangle OAB$ において，$\overrightarrow{a}=\overrightarrow{OA}$ ,$\overrightarrow{b}=\overrightarrow{OB}$ とする．

$\left|\overrightarrow{a}\right|=3$ , $\left|\overrightarrow{b}\right|=5$ , $\cos\angle AOB=\displaystyle\frac{3}{5}$

とする．このとき，$\angle AOB$ の $2$ 等分線と，$B$ を中心とする半径 $\sqrt{10}$ の円との交点の，$O$ を原点とする位置ベクトルを $\overrightarrow{a}$ , $\overrightarrow{b}$ を用いてあらわせ．

【2007大阪大学】

$xy$ 平面において，原点 $O$ を通る半径 $r$ ( $r>0$ ) の円を $C$ とし，その中心を $A$ とする．$O$ を除く $C$ 上の点 $P$ に対し，次の条件 $(a)$ , $(b)$ で定まる点 $Q$ を考える．

$(a)$　$\overrightarrow{OP}$ と $\overrightarrow{OQ}$ は向きが同じ．

$(b)$　$\left|\overrightarrow{OP}\right|\left|\overrightarrow{OQ}\right|=1$．

以下の問いに答えよ．

(１)　点 $P$ が $O$ を除く $C$ 上を動くとき，点 $Q$ は $\overrightarrow{OA}$ に直交する直線上を動くことを示せ．

(２)　(１)の直線を $l$ とする．$l$ が $C$ と $2$ 点で交わるとき， $r$ のとりうる値の範囲を求めよ．

【2009京都大学】

$xyz$ 平面上の $2$ 点 $A(-3,-1,1)$ , $B(-1,0,0)$ を通る直線 $l$ に点 $C(2,3,3)$ から下ろした垂線の足 $H$ の座標を求めよ．

【2022慶應義塾大学・商学部】

点 $O$ を原点とする $xyz$ 座標空間に，$2$ 点 $A ( 2 , 3 , 1 )$ , $B ( -2 , 1 , 3 )$ をとる．また，$x$ 座標が正の点 $C$ を，$\overrightarrow{OC}$ が $\overrightarrow{OA}$ と $\overrightarrow{OB}$ に垂直で，$\left|\overrightarrow{OC}\right|=8\sqrt{3}$ となるように定める．

(１)　$\triangle OAB$ の面積を求めよ．

(２)　点 $C$ の座標を求めよ．

(３)　四面体 $OABC$ の体積を求めよ．

(４)　平面 $ABC$ の方程式を求めよ．

(５)　原点 $O$ から平面 $ABC$ に垂線 $OH$ を下ろしたときの点 $H$ の座標を求めよ．

【2021九州大学・理】

座標空間内の $4$ 点 $O(0,0,0)$ , $A(1,0,0)$ , $B(0,1,0)$ , $C(0,0,2)$ を考える．以下の問に答えよ．

(１)　四面体 $OABC$ に内接する球の中心の座標を求めよ．

(２)　中心の $x$ 座標，$y$ 座標，$z$ 座標がすべて正の実数であり，$xy$ 平面，$yz$ 平面，$zx$ 平面のすべてと接する球を考える．この球が平面 $ABC$ と交わるとき，その交わりとしてできる円の面積の最大値を求めよ．

【4STEP(数学B)56】

$\triangle ABC$ と点 $P$ に対して，等式 $5\overrightarrow{AP}+4\overrightarrow{BP}+3\overrightarrow{CP}=\overrightarrow{0}$ が成り立っている．

(１)　点 $P$ がの位置をいえ．

(２)　$\triangle PBC : \triangle PCA : \triangle PAB$ を求めよ．