
教科書ではあまり教わることがありませんが、数学の2次試験では多くの大学で出題される頻出テーマの1つです。
確率漸化式の問題が解けるようになるためには
① 確率漸化式の問題であると気がつく
② 式を立てる
③ 漸化式を解く
の3つの力が必要。
そして多くの受験生がつまずくのは、「①確率漸化式の問題であると気がつく」こと。
ここでは最初に、どのような流れで確率漸化式の問題であると疑えるようになるか、気がつけるかと言うことをお話しします。
その上で、様々な例題を元に、「②式を立てる」ことに特化して、式の立て方、考え方について扱います。
③についてはここでは省略します。
①確率漸化式の考え方(最後の1手で場合分けのタイプ)
例題①(確率漸化式の問題であることに気がつくための考え方)

一般化された問題
👉 具体化・実験
方針がつかめない時は、まずは手を動かしましょう!
その際に、n=3〜5などの小さな例で実験を行ったあと、n=10や20といった大きな例で応用が効くのかを考えてください。何か規則性があり、それで問題が解ければOK!
とりあえず n=3 で実験してみました。
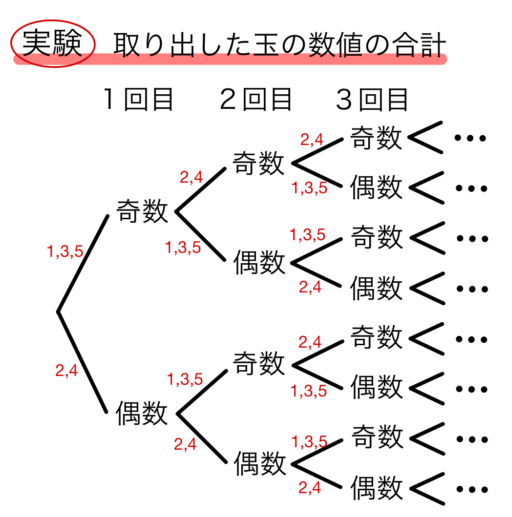
今回実験をしてみた結果、n の値が小さい時は頑張れば出来ますが、n の値が大きくなると、ずっと追いかけていくことは非常に厄介。
そこで
1回目からの動きを追いかけるのが大変
👉 漸化式の利用
という発想で漸化式が使えないか?と疑えるようにしましょう!
絶対にダメな勉強方法は、「確率漸化式の問題だ」と言う前提で演習をすること。
それではそもそも漸化式を利用すると言う発想になりません。
次に、漸化式を利用しようと思った後のお話し。
確率漸化式
👉(ⅰ)初めの1手で場合分け
(ⅱ)最後の1手で場合分け
※確率の全体が”1”であることを上手に使う
それぞれのケースについて以下では例題を用いて解説していきます。
ちなみに参考
まずは(ⅱ)の最後の1手で場合分けのタイプができるよになりましょう!
それでは改めて例題①について立式までの考え方を
例題①(立式の仕方)最後の1手で場合分け

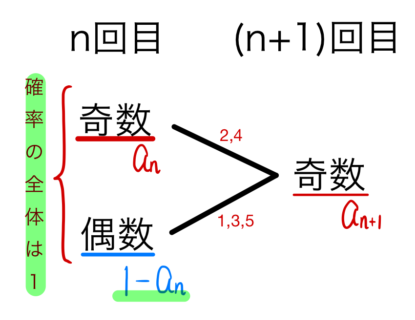
(👆このような図を推移図という)

推移図を書いて視覚的に!
例題② 最後の1手で場合分け

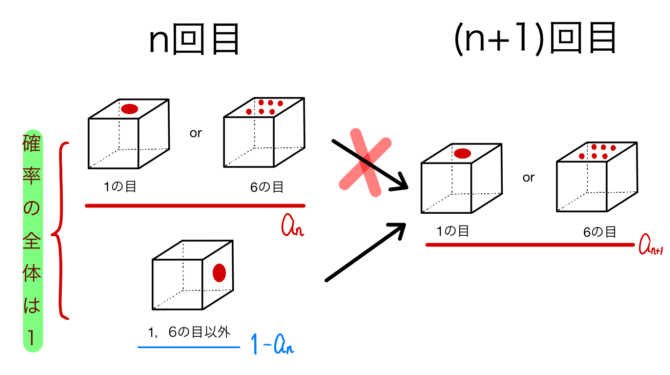
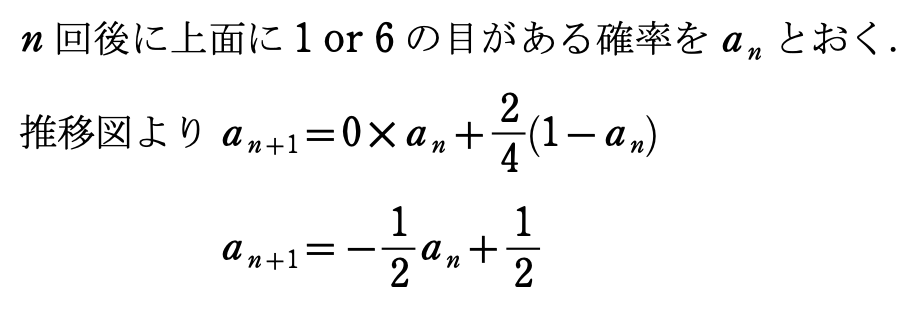
例題③ 2005京都大学(最初の1手で場合分け)

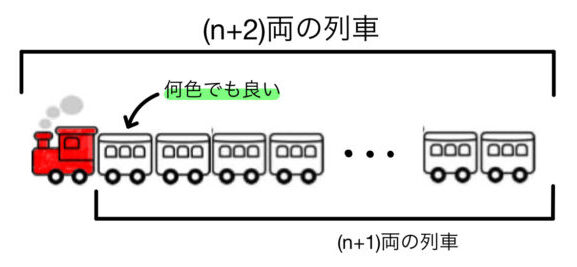
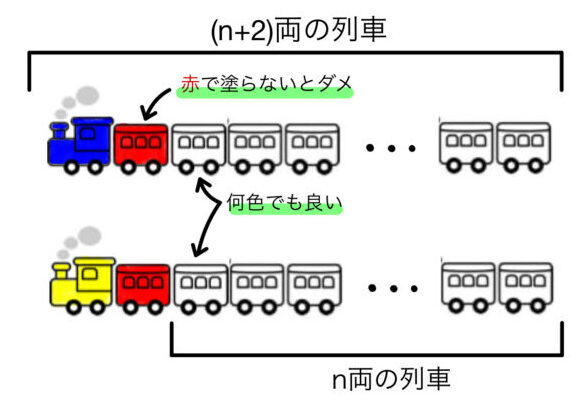

練習問題 5問



練習問題 解答


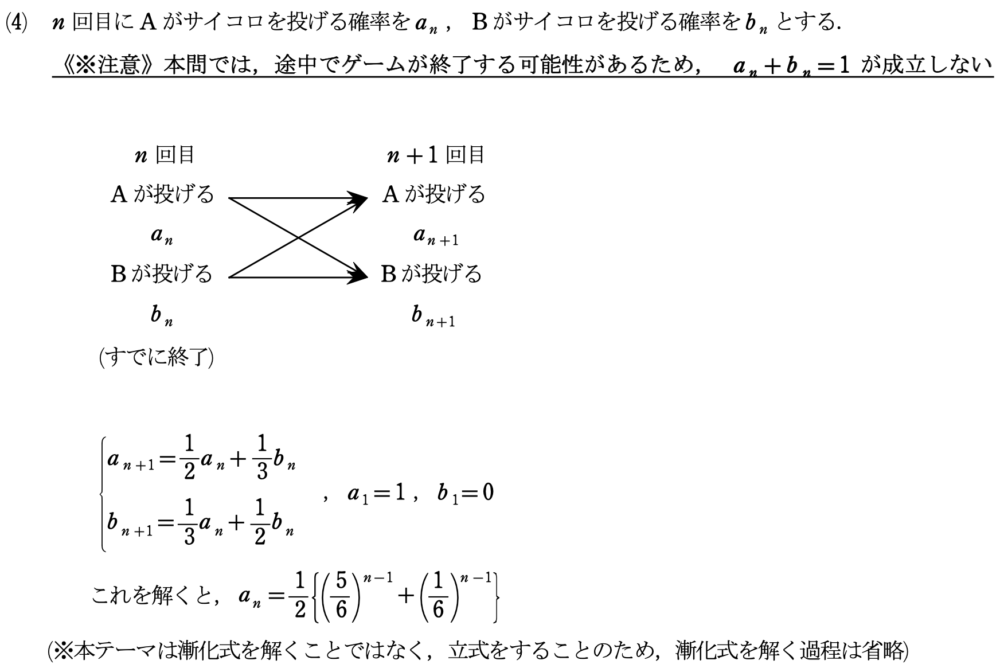







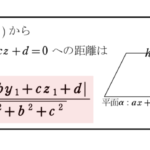
コメント