 式と証明
式と証明 相加平均・相乗平均の関係はいつ使う?使うタイミングの見抜き方(発展)
相加平均・相乗平均の関係は受験数学でも頻出で最重要分野の1つ。ただ公式を覚えているだけではダメ。どのタイミングで使うのかをしっかりとマスターしましょう!
 式と証明
式と証明  式と証明
式と証明  2次関数
2次関数 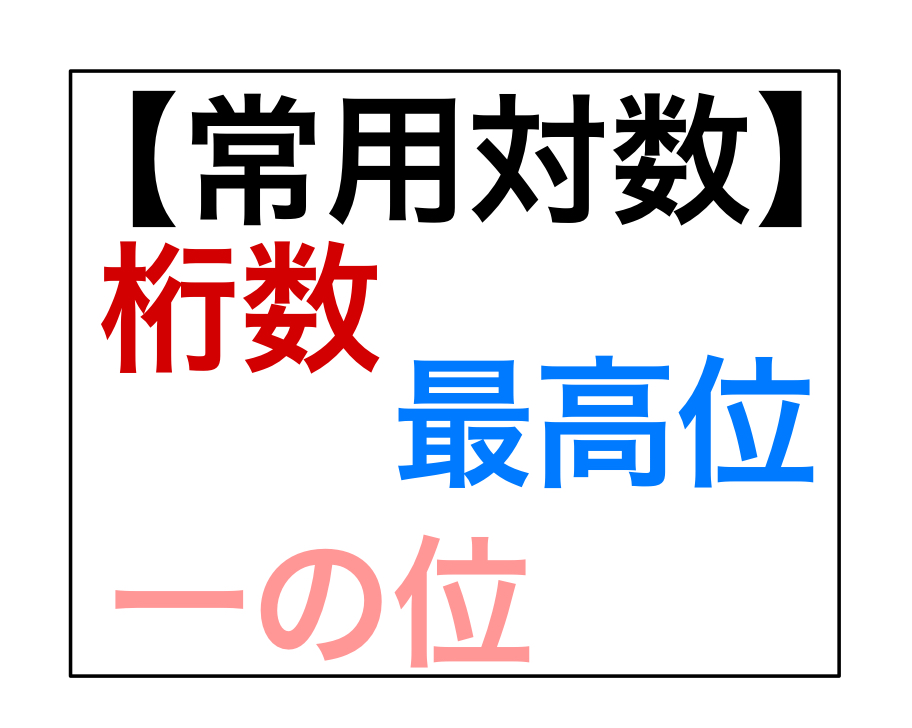 指数・対数関数
指数・対数関数 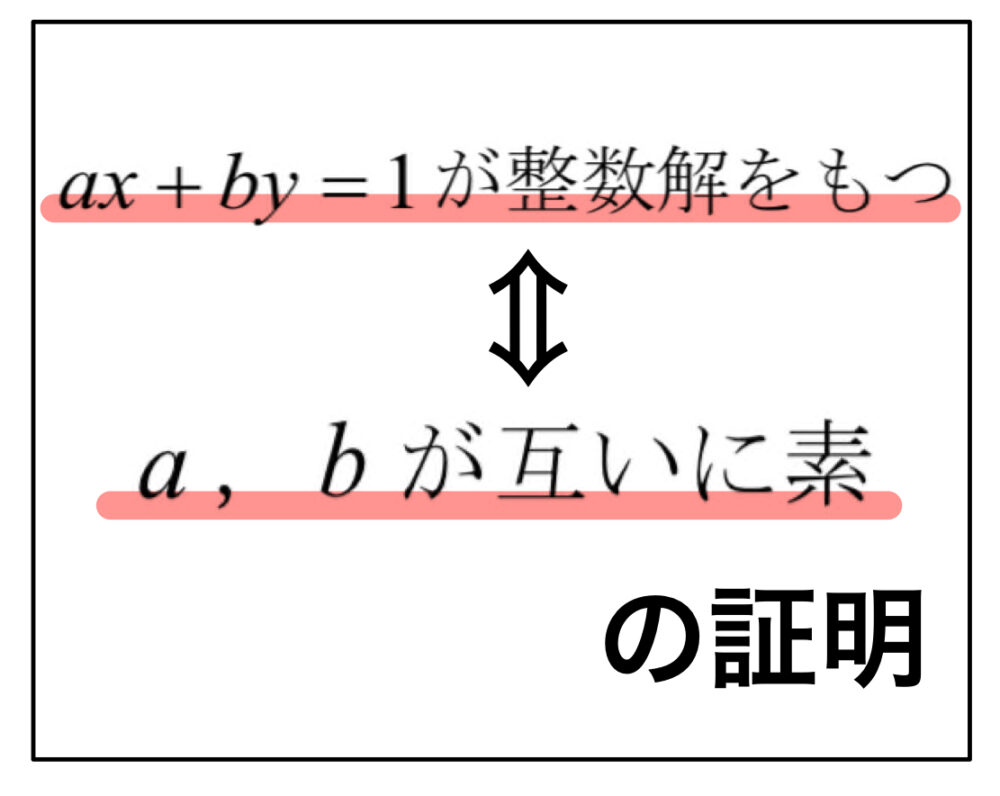 整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  東京大学
東京大学  整数問題
整数問題  東京大学
東京大学  整数問題
整数問題  共通テスト(センター試験)
共通テスト(センター試験)  共通テスト(センター試験)
共通テスト(センター試験)  整数問題
整数問題  図形と方程式
図形と方程式  整数問題
整数問題  集合と命題
集合と命題  分野まとめ
分野まとめ  京都大学
京都大学 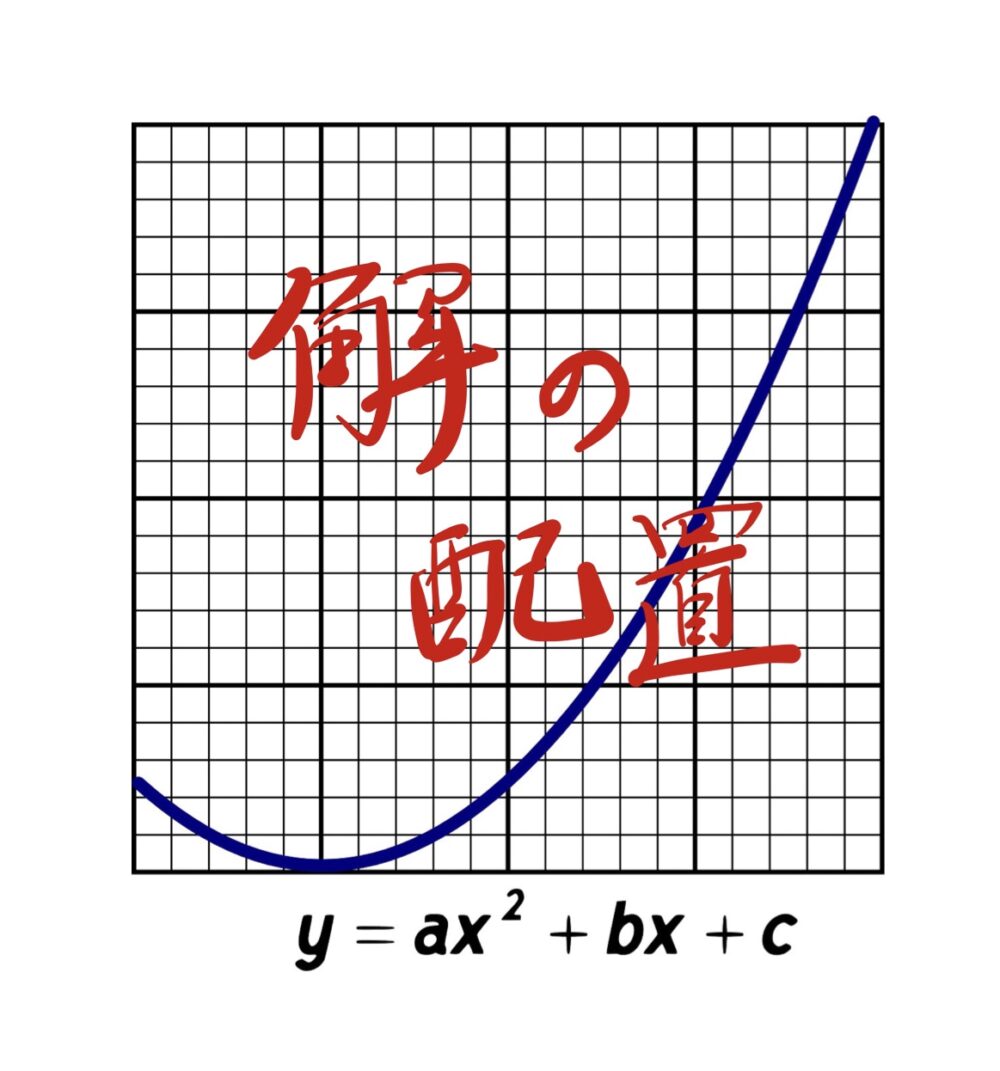 2次関数
2次関数  2次関数
2次関数 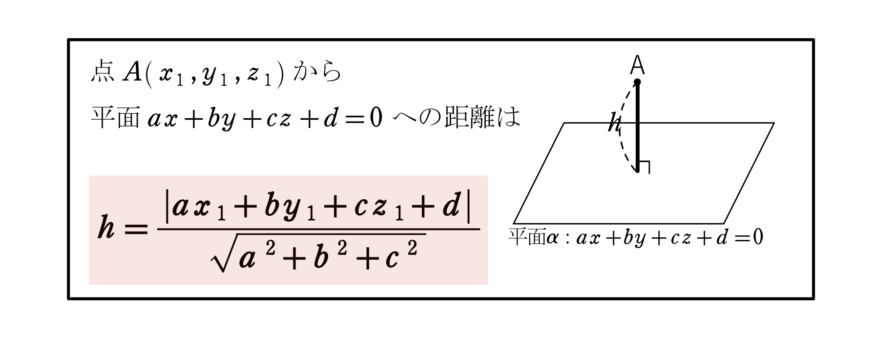 ベクトル
ベクトル  場合の数・確率
場合の数・確率