 共通テスト(センター試験)
共通テスト(センター試験) 【2022共通テスト】数学ⅠA:第2問[1](2次関数、集合と命題)|会話形式
2次方程式の実数解の個数。会話形式、誘導問題。文字定数を変化させてグラフの動きを考える。包含関係から必要条件、十分条件を考える。共通テスト・会話形式新傾向問題。大学共通テスト対策。センター試験過去問演習。数学ⅠA:2次関数、集合と命題
 共通テスト(センター試験)
共通テスト(センター試験)  共通テスト(センター試験)
共通テスト(センター試験)  共通テスト(センター試験)
共通テスト(センター試験)  共通テスト(センター試験)
共通テスト(センター試験)  整数問題
整数問題  整数問題
整数問題  数列
数列  数列
数列  東京大学
東京大学  2021年入試問題
2021年入試問題  ベクトル
ベクトル 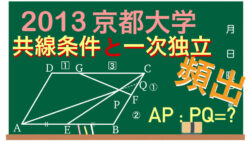 ベクトル
ベクトル  集合と命題
集合と命題 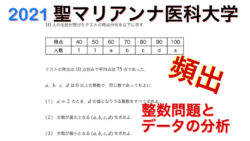 2021年入試問題
2021年入試問題  集合と命題
集合と命題  集合と命題
集合と命題  三角関数
三角関数  集合と命題
集合と命題  数列
数列  2次関数
2次関数  2次関数
2次関数  東京大学
東京大学  2次関数
2次関数  式と証明
式と証明