 整数問題
整数問題 【2009京都大学】pのn乗の階乗 は p で何回割り切れるか[整数・ガウス記号・頻出]
整数問題:頻出の2や3で何回割れるか、0が連続して何回並ぶかという問題の発展問題。すべて共通の考え方で、答えを求めるだけでなく、考え方・思考の仕方を解説。ガウス記号についても簡単に紹介。数学A2次試験対策。
 整数問題
整数問題  整数問題
整数問題  場合の数・確率
場合の数・確率  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  集合と命題
集合と命題  整数問題
整数問題 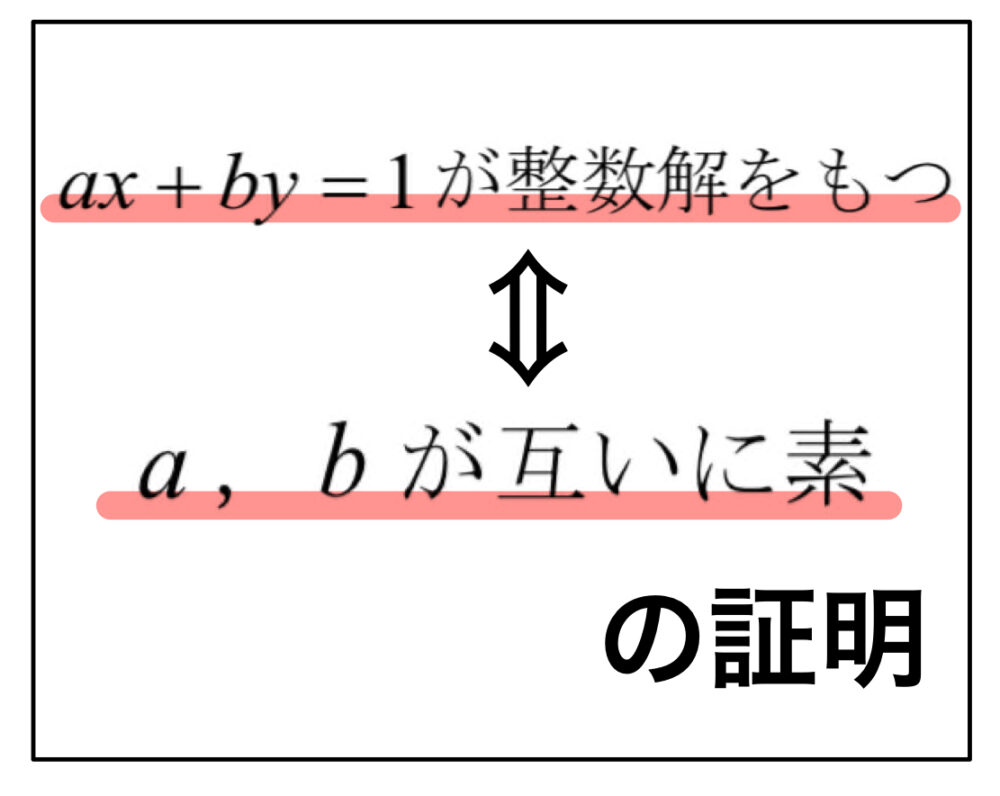 整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  東京大学
東京大学  整数問題
整数問題