【2022九州大学】
座標空間内の \(4\) 点 \(O(0,0,0)\) , \(A(1,1,0)\) , \(B(2,1,2)\) , \(P(4,0,-1)\)
を考える．\(3\) 点 \(O\) , \(A\) , \(B\) を通る平面を \(\alpha\) とし，\(\overrightarrow{a}=\overrightarrow{OA}\) , \(\overrightarrow{b}=\overrightarrow{OB}\) とおく．以下の問に答えよ．
(１) ベクトル \(\overrightarrow{a}\) , \(\overrightarrow{b}\) の両方に垂直であり，\(x\) 成分が正であるような，大きさが \(1\) のベクトル \(\overrightarrow{n}\) を求めよ．
(２) 点 \(P\) から平面 \(\alpha\) に垂線をおろし，その交点を \(Q\) とおく．線分 \(PQ\) の長さを求めよ．
(３) 平面 \(\alpha\) に関して点 \(P\) と対称な点 \(P^{\prime}\) の座標を求めよ．
平面の方程式，点と面の距離の公式，外積など，学校の授業では学習しないが，入試では頻出の知っておきたい差がつくテーマになります。ここでは基本的な問題を通して，使い方の演習をしていきましょう！
(１)外積の利用
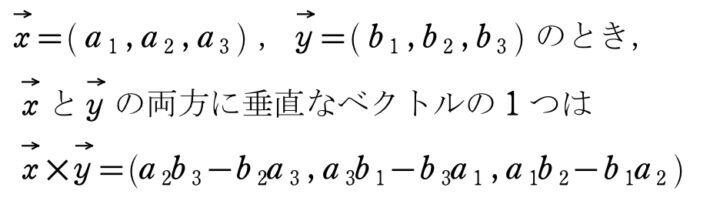
※ \(\vec{x}\times\vec{y}\) を \(\vec{x}\) と \(\vec{y}\) の外積という
※ 外積は高校数学では学習しません。（教科書に載っていません）そのため，記述式の答案で使用すると、減点される可能性があります。使用する場合は、記述として解答に残さないこと！
(１)解答
\(\overrightarrow{a}\) , \(\overrightarrow{b}\) の両方に垂直なベクトルの \(1\) つを \(\overrightarrow{x}\) とおくと，
\(\overrightarrow{x}=(2,-2,-1)\) であり，
\(\left|\overrightarrow{x}\right|=\sqrt{2^2+(-2)^2+(-1)^2}=3\) であるから，
求める \(\overrightarrow{n}\) は，\(\overrightarrow{n}=\displaystyle\frac{1}{3}\overrightarrow{x}=\left(\displaystyle\frac{2}{3},-\displaystyle\frac{2}{3},-\displaystyle\frac{1}{3}\right)\)
(２)平面の方程式・点と面の距離の公式
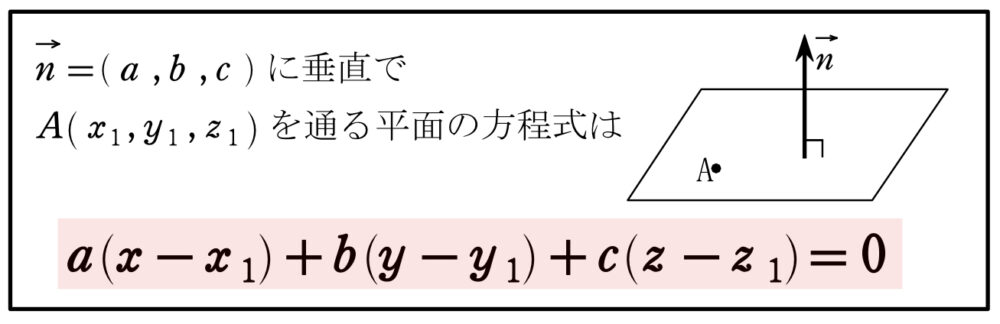
平面の方程式
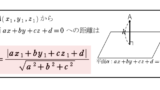
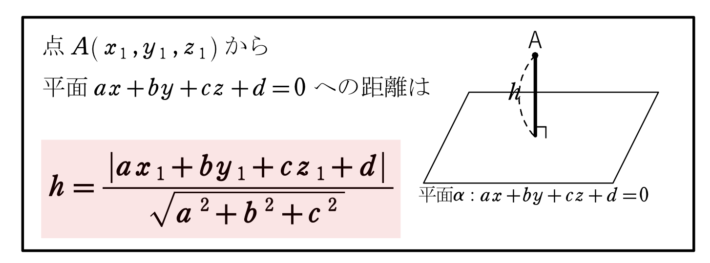
点と面の距離の公式
(２)解答
点 \(O\) を通り，\(\overrightarrow{x}=(2,-2,-1)\) に垂直な平面 \(\alpha\) の方程式は
\(2x-2y-z=0\) ・・・①
①と\(P(4,0,-1)\) の距離は
\(PQ=\displaystyle\frac{|2\times 4-2\times 0-(-1)|}{\sqrt{2^2+(-2)^2+(-1)^2}}=3\)
(３)平面に関して対称な点
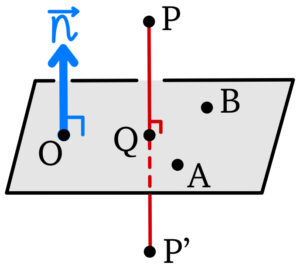実数 \(k\) を用いて
\(\overrightarrow{OQ}=\overrightarrow{OP}+k\overrightarrow{x}\) と表せるので
\(\overrightarrow{OQ}=(2k+4,-2k,-k-1)\) より
点 \(Q (2k+4,-2k,-k-1)\) となる．
ここで点 \(Q\) は，平面 \(\alpha\) 上より，①から
\(2(2k+4)-2(-2k)-(-k-1)=0\)
\(\iff\) \(k=-1\)
よって，\(Q (2,2,0)\)
ここで点 \(P\) と \(P^{\prime}\) の中点が \(Q\) より
\(\overrightarrow{OQ}=\displaystyle\frac{1}{2}(\overrightarrow{OP}+\overrightarrow{OP^{\prime}})\)
\(\overrightarrow{OP^{\prime}}=2\overrightarrow{OQ}-\overrightarrow{OP}\)
よって，\(\overrightarrow{OP^{\prime}}=2(2,2,0)-(4,0,-1)=(0,4,1)\)
したがって， \(P^{\prime}(0,4,1)\)
コメント