 ベクトル
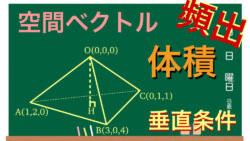
ベクトル 【頻出】四面体の体積|空間ベクトル(共面条件・垂直条件)
4点 O(0,0,0),A(1,2,0),B(3,0,4),C(0,1,1)でできる四面体OABCの体積の求め方。三角形のベクトルの最重要面積公式、共面条件、平面とベクトルの垂直条件(高さを求める)。数学B:空間ベクトル。平面の方程式、点と面の距離による別解。
 ベクトル
ベクトル 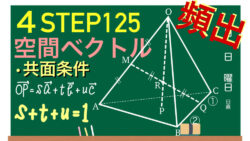 ベクトル
ベクトル 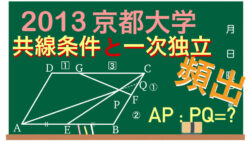 ベクトル
ベクトル  図形と方程式
図形と方程式 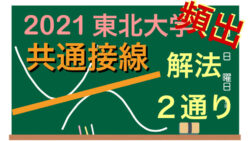 旧帝大(東大・京大除く)+3大学(一工神)
旧帝大(東大・京大除く)+3大学(一工神)  漸化式
漸化式  漸化式
漸化式  漸化式
漸化式  漸化式
漸化式  分野まとめ
分野まとめ  漸化式
漸化式  漸化式
漸化式  漸化式
漸化式  漸化式
漸化式  漸化式
漸化式  漸化式
漸化式  漸化式
漸化式  漸化式
漸化式  数列
数列  式と証明
式と証明  整数問題
整数問題  整数問題
整数問題  大学受験情報
大学受験情報  集合と命題
集合と命題