 複素数平面まとめ(数Ⅲ)
複素数平面まとめ(数Ⅲ) 【数Ⅲ】複素数平面まとめ①(絶対値について)|入試問題演習
①複素数平面(数学Ⅲ)における絶対値について2次試験対策。入試問題演習まとめ。様々なテーマごとに、ポイント、考え方、別解を解説。
 複素数平面まとめ(数Ⅲ)
複素数平面まとめ(数Ⅲ)  場合の数・確率
場合の数・確率  整数問題
整数問題  図形と方程式
図形と方程式  数列
数列  整数問題
整数問題  指数・対数関数
指数・対数関数  複素数と方程式
複素数と方程式  ベクトル
ベクトル  整数問題
整数問題  数列
数列  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  数学(大学入試問題)
数学(大学入試問題) 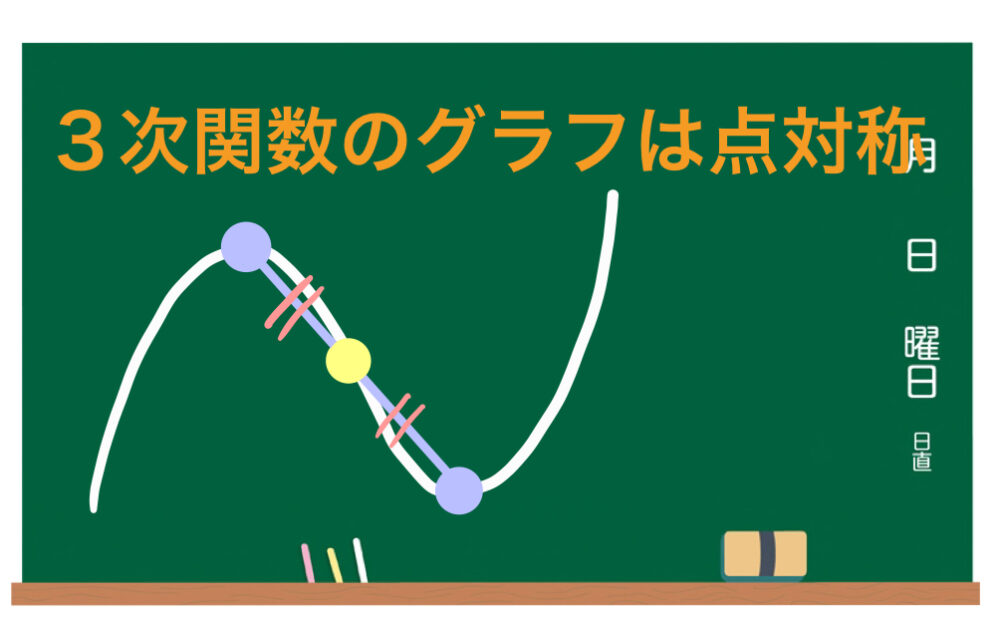 微分・積分
微分・積分  整数問題
整数問題  式と証明
式と証明  整数問題
整数問題  整数問題
整数問題  三角関数
三角関数  式と証明
式と証明  場合の数・確率
場合の数・確率  整数問題
整数問題